スポンサーリンク
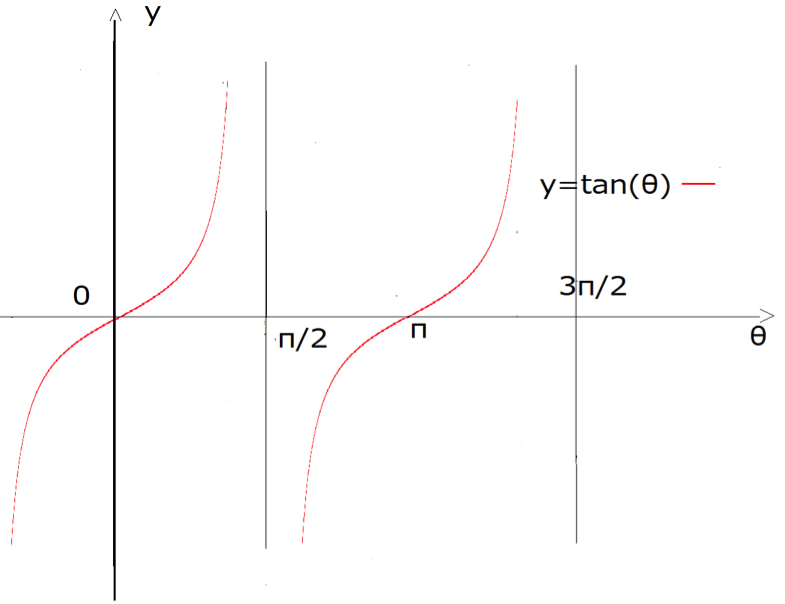
y=tan(θ) のグラフ (タンジェントのグラフ)
三角関数![]() のグラフは次のように書けます。
のグラフは次のように書けます。
y=tan(θ) のグラフ
y=tan(θ) のグラフの書き方 (タンジェントのグラフ)の解説/ポイント
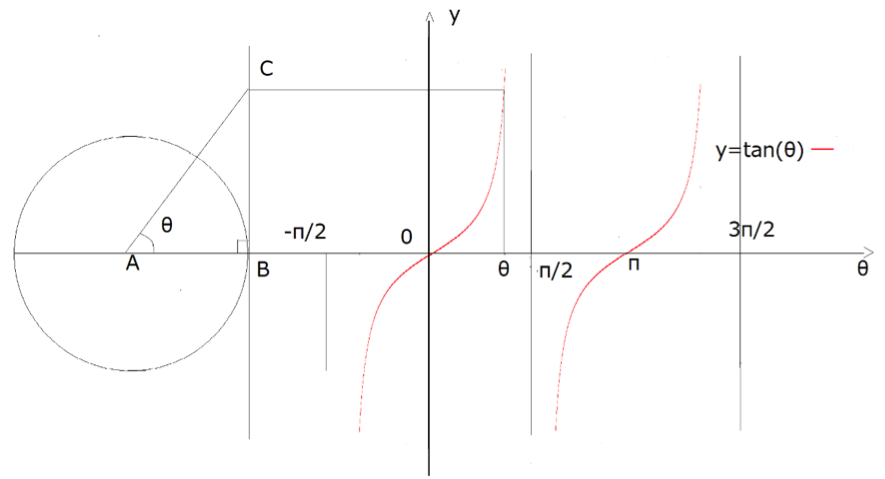
![]() のグラフを書くときにはまず下の図のように単位円を描くと書きやすくなります。
のグラフを書くときにはまず下の図のように単位円を描くと書きやすくなります。
y=tan(θ)のグラフの書き方
図のように、θ軸上に点A, Bをとり、点Bを通り単位円(半径1の円)の接線を書きます。
その接線上にCをとり、ABとACの角度を![]() とすると、三角比の定義より
とすると、三角比の定義より
![]()
![]()
![]()
![]()
と書けます。
ここで、CBを点Cのy 座標とみることもできます。よって、y=tan(θ) =(Cのy 座標) (ただし, ![]() は実数)とかけます。
は実数)とかけます。
ただし、θ=π/2+nπ(nは整数)の時tan(θ)は値をとらないことに注意して下さい。
上でBCの長さを点Cのy 座標と言い換えた理由は, そのままでは![]() の範囲以外では定義されていないためです。
の範囲以外では定義されていないためです。
というのもいままで三角比の定義で考えていた ![]() は
は ![]() だけでした。
だけでした。
また, この三角関数のグラフから, ![]() となることが確認できます。
となることが確認できます。
y=tan(θ) のグラフの書き方の例題
問題
![]() のグラフを参考に次の等式を完成させなさい。
のグラフを参考に次の等式を完成させなさい。
![]()
![]()
解答
図の単位円に立ち返って考えてみると、
![]()
の時の各々の点Cの位置は一致するので
![]()
が成立します。
よって、グラフと合わせて、
![]()
となります。
参考
「数学Ⅱ 川中 宣明著 数研出版」