- 平行移動や対称移動で移動した後の関数から、移動する前の関数を求める問題です。
- 平行移動する前の関数は、逆向きに平行移動することで求められます。
- 対称移動する前の関数は、もう一度対称移動することで求められます。
スポンサーリンク
移動前の二次関数を求める問題
ある二次関数を![]() 軸方向に
軸方向に![]() 、
、![]() 軸方向に
軸方向に![]() だけ平行移動し、原点に関して対称移動したところ、
だけ平行移動し、原点に関して対称移動したところ、
![]() となった。元の二次関数を求めなさい。
となった。元の二次関数を求めなさい。
平行移動・対称移動から解法の導く手順
- 移動した後の関数を、原点に関して対称移動します。
- 原点に関して対称移動した関数を、
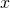 軸方向に
軸方向に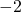 、
、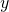 軸方向に
軸方向に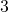 だけ平行移動します。
だけ平行移動します。
移動前の二次関数を求める問題の解説
移動を逆にたどることで、移動前の関数が求められます。
この問題では (元の関数)![]() 平行移動
平行移動![]() 対称移動
対称移動![]()
![]() となっているので、まずは対称移動する前の関数を求めます。
となっているので、まずは対称移動する前の関数を求めます。
対称移動を2回行うと元の関数に戻るので、
![]() をもう一度原点に関して対称移動することで、対称移動する前の関数が求められます。
をもう一度原点に関して対称移動することで、対称移動する前の関数が求められます。
この関数は![]() をそれぞれ
をそれぞれ![]() に置き換えることで
に置き換えることで
![]()
![]()
と求められます。
次に、平行移動する前の関数を求めます。
平行移動する前の関数は逆向きの平行移動をすることで求められるので、
![]() 軸方向に
軸方向に![]() 、
、![]() 軸方向に
軸方向に![]() だけ平行移動します。
だけ平行移動します。
![]() をそれぞれ
をそれぞれ![]() に置き換えることで平行移動した関数が求められ、
に置き換えることで平行移動した関数が求められ、
![]()
![]()
となります。
よって、元の関数は
![]()
と求めることができます。
参考
数学1教科書 数研出版