正弦定理の公式の証明：図形と計量

正弦定理の公式

正弦定理

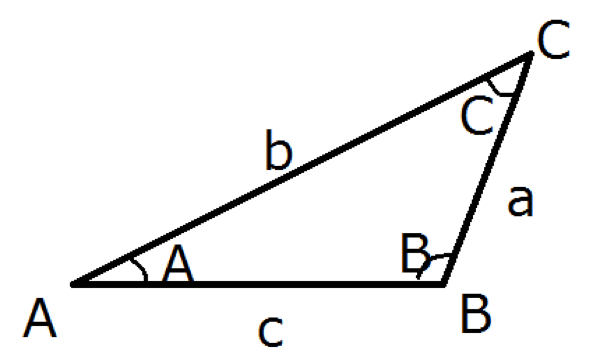
図のような三角形ABCに対して外接円の半径をRとすると, 次の等式が成立します。
これを正弦定理と呼びます。

$\begin{eqnarray} \dfrac{a}{sinA}\end{eqnarray}$

$\begin{eqnarray}= \dfrac{b}{sinB} \end{eqnarray}$

$\begin{eqnarray}= \dfrac{c}{sinC}\end{eqnarray}$

$\begin{eqnarray}= 2R \end{eqnarray}$

正弦定理の証明

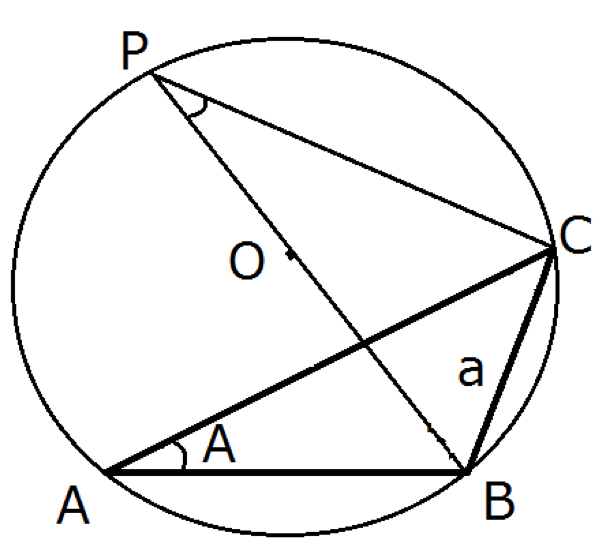
図のように三角形ABCの外接円を書き, その円の中心をOとしてOBと外接円の交点を図のようにPとおきます。外接円の性質より, ∠BAC＝∠BPCとなります。またBPが円の直径になっていることに着目すると, ∠PCBは直角になります。よって直角三角形PCBについて注目すると

$a=BC=BP sin(∠BPC)=2R sinA$

となります。つまり

$\dfrac{a}{sinA}=2R$

となります。同様にして

$\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R$

が証明できます。
また, 今回は角Aは鋭角ですが, 鈍角のものでも同様にして証明することができます。

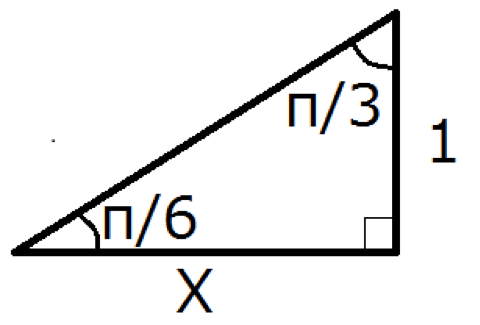
次の三角形について, 辺の長さXを求めなさい。

正弦定理の例題

正弦定理より

$\dfrac{1}{sin(\pi / 6)}= \dfrac{X}{sin(\pi / 3)}$

を満たすので,

$X=1\times \dfrac{ sin(\pi / 3)}{sin(\pi / 6)}= \dfrac{ 1}{~\sqrt[]{\mathstrut 3}}$

となります。

「新課程チャート式基礎からの数学Ⅰ＋A チャート研究所編著数研出版」