原点と直線の距離の公式の証明：図形と計量

2016/2/14 2016/3/5 図形と計量, 図形と計量, 数学, 数学Ⅰ

スポンサーリンク

原点と直線の距離の公式

原点 $O(0, 0)$ と直線 $B;ax+by+c=0$ の距離 T は

$\begin{eqnarray<em>} T=\dfrac{| c|}{~\sqrt[]{\mathstrut a^2+b^2}} \end{eqnarray</em>}$

となります。

原点と直線の距離の公式の証明の解説/ポイント

まず原点からの距離を調べます。

直線BとOの距離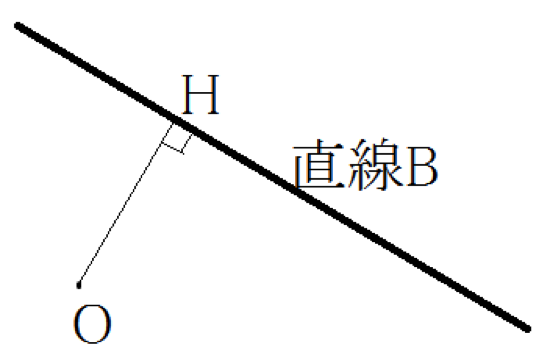原点と直線の距離の求め方

上の図のように点Oから直線Bに垂線をおろし, その足をHとします。
ここで一旦, $b, a\ne 0$ として直線OHを求めます。
この時直線Bは

$y=-\dfrac{a}{b}x-\dfrac{c}{b}$

と書けるので
傾きは $-\dfrac{a}{b}$ となります。
また, 直線OHと直線Bは直行しているので,
直線OHの傾きをSとすると,

$-\dfrac{a}{b}S=-1$

を満たすので

$\dfrac{b}{a}=S$

と書けます。
よって直線OHは未知数Tを用いて

$y=\dfrac{b}{a}x+T$

と書けます。
この直線OTは点 $O(0, 0)$ を通るので $0=T$ を満たします。
以上のことから直OHは

$y=\dfrac{b}{a}$

より

$ay-bx=0$

となります。
これは $b, a= 0$ のときも, 上の式を満たします。
たとえば直線Bを $b=0$ つまり $x=0$ とすると,
直線OHはy=0となります。

　次に, Hの座標を求めます。点Hは直線Bと直線OHの交点なので連立方程式

$ax+by+c=0$

$ay-bx=0$

の解になります。

これに対して各々bとaをかけると

$bax+bby+bc=0$

$aay-abx=0$

この2つの式の両辺を足すと

$\begin{eqnarray<em>} (a^2+b^2)y+bc=0 \end{eqnarray</em>}$

となります。

よって

$y=\dfrac{-bc}{a^2+b^2}$

これを $ay-bx=0$ に代入すると,

$x=\dfrac{-ac}{a^2+b^2}$

となります。

よって, 点Hの座標は

$\begin{eqnarray<em>} 点H (\dfrac{-ac}{a^2+b^2}, \dfrac{-bc}{a^2+b^2}) \end{eqnarray</em>}$

となります。

よって2点間の距離の公式よりOHの距離は

$\begin{eqnarray<em>} \sqrt[]{\mathstrut \left{\dfrac{-ac}{a^2+b^2}\right}^2+ \left{\dfrac{-bc}{a^2+b^2}\right}^2 }\end{eqnarray</em>}$

$\begin{eqnarray<em>}=\sqrt[]{\mathstrut \dfrac{c^2}{a^2+b^2} }\end{eqnarray</em>}$

$\begin{eqnarray<em>}=\dfrac{|c|}{\sqrt[]{\mathstrut a^2+b^2}} \end{eqnarray</em>}$

と, 求めたかった式が出てきました。

原点と直線の距離の求め方の公式の例題

問題

原点 $(0, 0)$ と直線 $3x+4y+4=0$ の距離を求めなさい。

解答

点と直線の距離の公式より,

$\begin{eqnarray<em>} \dfrac{4}{\sqrt[]{\mathstrut 3^2+4^2} } =\dfrac{4}{5} \end{eqnarray</em>}$

となります。

参考

「新課程チャート式基礎からの数学Ⅱ＋B チャート研究所編著数研出版」

関連記事

スポンサーリンク