三角関数の合成を利用して最大値・最小値を求めるの問題のポイント：三角関数

2016/3/4 2016/3/5 三角関数, 数学, 数学Ⅱ

スポンサーリンク

三角関数の合成を利用して最大値・最小値を求めるの問題のポイント

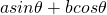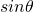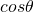$a sin\theta +b cos\theta$ の形で表される、 $sin\theta$ と $cos\theta$ の和が含まれる三角関数の最大値と最小値を求める問題です。
三角関数の合成を行い、関数の式を 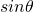$sin\theta$ だけを用いて表します。
合成で置き換えた 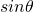$sin\theta$ の取りうる値の範囲に注意します。

三角関数の合成の問題

関数 $y=-2 sin2x+2 cos2x+3$ の最大値と最小値を求めよ。ただし $0 \leqq x \leqq \dfrac{\pi}{2}$ とする。

《2014年度岩手大学入試問題》

三角関数の合成の解法の手順

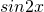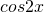$sin2x$ と $cos2x$ を合成します。
合成によってできた 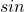$sin$ の値の範囲を求めます。
2で求められた範囲での、最大値と最小値を求めます。

三角関数の合成の問題の解説

$sinとcos$ の和や差が含まれる場合、三角関数の合成を用いて $sin$ だけで式を表すことで
最大値と最小値が求められます。
与えられた関数に含まれる、 $-2 sin2x+2 cos2x$ を合成すると

$~\sqrt[]{\mathstrut (-2)^2+2^2 }=2~\sqrt[]{\mathstrut 2}$

より

$-2 sin2x+2 cos2x$

$=2~\sqrt[]{\mathstrut 2} \left(\dfrac{-1}{~\sqrt[]{\mathstrut 2}} sin2x+\dfrac{1}{~\sqrt[]{\mathstrut 2}} cos2x \right)$

$=2~\sqrt[]{\mathstrut 2} sin\left(2x+\dfrac{3}{4}\pi\right)$

となります。よって、

$y=-2 sin2x+2 cos2x+3$

$y=2~\sqrt[]{\mathstrut 2} sin\left(2x+\dfrac{3}{4} \pi\right)+3$

と変形できます。次に、 $sin\left( 2x+\dfrac{3}{4} \pi \right)$ の値の範囲を求めます。
$0 \leqq x \leqq \dfrac{\pi}{2}$ より $0 \leqq 2x \leqq \pi$ となります。よって、

$\dfrac{3}{4} \pi \leqq 2x+\dfrac{3}{4} \pi \leqq \dfrac{7}{4} \pi$

なので、

$-1 \leqq sin \left(2x+\dfrac{3}{4} \pi \right) \leqq \dfrac{1}{~\sqrt[]{\mathstrut 2}}$

となります。よって、

$sin \left(2x +\dfrac{3}{4} \pi \right)= \dfrac{1}{~\sqrt[]{\mathstrut 2}}$

すなわち x=0のとき最大値5

$sin\left(2x +\dfrac{3}{4} \pi \right) =-1$

すなわち

$x=\dfrac{3}{8} \pi$

のとき最小値

$&&3-2~\sqrt[]{\mathstrut 2}$

と求められます。

引用

2014年度岩手大学入試問題

参考

チャート式　数研出版

関連記事

スポンサーリンク