定積分で表された関数の決定問題の解法ポイント：積分

2016/3/2 2016/3/5 微分・積分, 数学, 数学Ⅱ

スポンサーリンク

定積分で表された関数の決定問題の解法ポイント

定積分 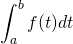$\displaystyle \int_a^bf(t)dt$ が式中に含まれる関数 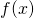$f(x)$ を求める問題です。
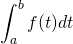$\displaystyle \int_a^bf(t)dt$ は定積分なので定数として扱い、関係式を解きます。

定積分で表された関数の問題

次の等式を満たす関数 $f(x)$ を求めなさい。

$f(x)=x^2+\int_0^1(x+t)f(t)dt$

定積分で表された関数の決定の解法の手順

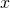$x$ を定積分の外に出します。
定積分の部分を定数に置き換えます。
定数に置き換えて表した関数を、定積分に代入します。
関係式を解いて、定数の値を求めます。

定積分で表された関数の問題の解説

定積分中の式を展開すると、

$f(x)=x^2+\int_0^1(x+t)f(t) dt$

$=x^2+\int_0^1\Bigl(xf(t)+tf(t)\Bigl) dt$

$=x^2+\int_0^1xf(t) dt+\int_0^1tf(t) dt$

となります。
ここで、 $\displaystyle \int_0^1xf(t) dt$ は $t$ の定積分なので、 $x$ は定数として定積分の外に出すことができます。
よって、

$f(x)=x^2+\int_0^1xf(t) dt+\int_0^1tf(t) dt$

$=x^2+x\int_0^1f(t) dt+\int_0^1tf(t) dt$

と変形できます。
次に、 $\displaystyle \int_0^1f(t) dt$ と $\displaystyle \int_0^1tf(t) dt$ は定積分なので、 $t$ を含まない定数となります。

よって、 $\displaystyle \int_0^1f(t) dt=a$ , $\displaystyle \int_0^1tf(t) dt=b$ と置き換えて

$f(x)=x^2+x\int_0^1f(t) dt+\int_0^1tf(t) dt$

$=x^2+ax+b$

と表すことができます。
$f(x)$ を $x$ と定数 $a,b$ を用いて表すことができたので、これを
$\displaystyle \int_0^1f(t) dt=a$ , $\displaystyle \int_0^1tf(t) dt=b$ に代入して、 $aとb$ の関係式を導きます。

$\displaystyle \int_0^1f(t) dt=a$ より

$\int_0^1(t^2+at+b)dt=a$

$\left[\dfrac{1}{3} t^3+\dfrac{a}{2} t^2+bt \right]_0^1=a$

$\dfrac{1}{3}+\dfrac{a}{2}+b=a$

$\dfrac{a}{2}-b=\dfrac{1}{3} \dots (1)$

が得られます。同様にして、 $\displaystyle \int_0^1tf(t) dt=b$ より

$\int_0^1t(t^2+at+b)dt=b$

$\int_0^1(t^3+at^2+bt)dt=b$

$\left[\dfrac{1}{4} t^4+\dfrac{a}{3} t^3+\dfrac{b}{2} t^2 \right]_0^1=b$

$\dfrac{1}{4} +\dfrac{a}{3}+\dfrac{b}{2} =b$

$\dfrac{a}{3}-\dfrac{b}{2} =-\dfrac{1}{4} \dots (2)$

が得られます。(1)、(2)を連立方程式として解くと

$a=-5,b=-\dfrac{17}{6}$

が得られるので、 $f(x)=x^2+ax+b$ に代入して

$f(x)=x^2-5x-\dfrac{17}{6}$

が求められます。

参考

チャート式　数研出版

関連記事

スポンサーリンク