3次関数の最大値・最小値を求める際のポイント：微分法

3次関数の最大値・最小値を求める際のポイント

• 3次以上の関数について、定義域内での最大値と最小値を求める問題です。
• 微分を利用して極大値と極小値を求め、定義域の両端での値と比較します。

3次関数の最大値・最小値を求める問題

次の関数の最大値と最小値を求めよ。

   

   

3次関数の最大値・最小値の解法の手順

1. 微分して、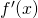を求めます。
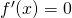2. を満たす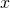の値を求めます。
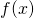3. の増減を調べ、極大値と極小値を求めます。
4. 定義域の両端での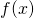の値を求めます。
5. 極大値・極小値と定義域の両端での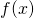の値を比較し、最大値と最小値を求めます。

3次関数の最大値・最小値の問題の解説

3次以上の関数の場合、最大値と最小値を求めるには微分を利用します。

   

   

よって、となるのはのときであり、増減は以下のようになります。

増減表

よって、のときに極大となり、極大値はとなります。また、
のときに極小となり、極小値はとなります。
次に、定義域がなので、のときのの値を求めると、

   

   

となるので、のとき最大値、のとき最小値となります。

参考

数学2教科書　数研出版