1次の対数方程式の解法ポイント：対数関数

2016/3/4 2016/3/13 指数関数と対数関数, 数学, 数学Ⅱ

対数で表された項を含む方程式を解く問題です。
両辺の項の底を揃え、 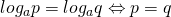$log_ap=log_aq \Leftrightarrow p=q$ を利用します。
得られた解が真数条件を満たしているかに注意します。

スポンサーリンク

1次の対数方程式の問題

方程式 $log_2(x-1)-log_4(x+11)=0$ を解け。

1次の対数方程式の解法の手順

真数条件から、解の値の範囲を求めます。
対数の底を揃えます。
すべての項が正になるように移項します。
両辺をそれぞれ一つの対数に変形します。
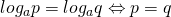$log_ap=log_aq \Leftrightarrow p=q$ を利用して対数を外します。
方程式を解き、得られた解が1の範囲に含まれるかを確かめます。

1次の対数方程式の問題の解説

まず、真数条件から解の値の範囲を求めます。
$x-1>0よりx>1$ 、 $x+11>0よりx>-11$ となるので、
解の値の範囲はこの2つの共通部分である

$x>1$

となります。次に、底の変換公式を利用して2つの項の底を揃えます。

$log_2(x-1)-log_4(x+11)=0$

$log_2(x-1)-\dfrac{log_2(x+11)}{log_24} =0$

$log_2(x-1)-\dfrac{log_2(x+11)}{2}=0$

と変形できます。係数が負の項を残して変形を続けると方程式に分数が含まれてしまうので、 $-\dfrac{log_2(x+11)}{2}$ を移項してすべての項が正になるようにします。

$log_2(x-1)=\dfrac{log_2(x+11)}{2}$

次に、両辺をそれぞれ1つの対数だけで表します。
右辺の分母を払い、 $n log_ap=log_ap^n$ を用いて左辺の対数に組み入れます。

$2 log_2(x-1)=log_2(x+11)$

$log_2(x-1)^2=log_2(x+11)$

両辺を底が同じ対数で表すことができたので、 $log_ap=log_aq\Leftrightarrow p=q$ を利用して対数を外します。

$(x-1)^2=x+11$

整理して

$x^2-3x-10=0$

$(x+2)(x-5)=0より$

$x=-2,5$

最後に、ここで得られた解が、最初に求めた解の値の範囲に含まれるかを確かめます。

$x>1$ より
$x=-2$ は不適なので、解は $x=5$ となります。

参考

数学Ⅱ教科書　数研出版
チャート式　数研出版

関連記事

スポンサーリンク