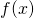２つの定積分から関数を求める際の解法のポイント：積分　

2016/3/4 2016/3/5 微分・積分, 数学, 数学Ⅱ

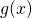$f(x)$ と $g(x)$ の定積分が式中に含まれる2つの関数 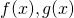$f(x),g(x)$ を求める問題です。
定積分を定数に置き換え、得られる関係式を解きます。
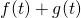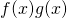2つの関数の和 $f(t)+g(t)$ や積 $f(x)g(x)$ の定積分の置き換え方に注意します。

スポンサーリンク

２つの定積分から関数を求める問題

次の等式を同時に満たす関数 $f(x),g(x)$ を求めなさい。

$f(x)=x^2+\int_0^1\Bigl(f(t)+g(t)\Bigr)dt$

$g(x)=x+\int_0^1f(t)g(t)dt$

２つの定積分から関数を求める解法の手順

和、積をそのままで定数に置き換えます。
定数に置き換えて表した関数を、定積分に代入します。
関係式を解いて、定数の値を求めます。

２つの定積分から関数を求める問題の解説

関数が1つの場合と同様に、定積分を定数に置き換えて関係式を解きます。この問題のように2つの関数の積の定積分がある場合、積を1つの関数とみて1つの定数に置き換えます。また、和に関しても一方の定積分だけで表された式がないので、まとめて1つの定数に置き換えると計算が簡単になります。

$\int _0^1\Bigl(f(t)+g(t)\Bigr)dt=a$

$\int _0^1f(t)g(t)dt=b$

と置くと、

$f(x)=x^2+a,g(x)=x+b$

と表せます。2つの関数を $x$ と定数を用いて表すことができたので、関数が1つの場合と同様にこれらの式を定積分に代入して計算します。

$\int _0^1\Bigl(f(t)+g(t)\Bigr)dt=aより$

$\int _0^1\Bigl((t^2+a)+(t+b)\Bigr)dt=a$

$\left [\dfrac{1}{3} t^3+\dfrac{1}{2} t^2+(a+b)t \right]_0^1=a$

$\dfrac{1}{3}+\dfrac{1}{2}+a+b=a$

$b=-\dfrac{5}{6}$ が得られます。よって、 $g(x)=x-\dfrac{5}{6}$ となるので、

$\int _0^1f(t)g(t)dt=b$

より

$\int _0^1(t^2+a)(t-\dfrac{5}{6})dt=-\dfrac{5}{6}$

$\int _0^1(t^3-\dfrac{5}{6} t^2+at-\dfrac{5}{6} a)dt=-\dfrac{5}{6}$

$\left[\dfrac{1}{4} t^4-\dfrac{5}{18} t^3+\dfrac{1}{2} at^2-\dfrac{5}{6} at \right]_0^1=-\dfrac{5}{6}$

$\dfrac{1}{4}-\dfrac{5}{18}+\dfrac{1}{2} a-\dfrac{5}{6} a=-\dfrac{5}{6}$

$a=\dfrac{29}{12}$ が得られます。よって、 $f(x)=x^2+\dfrac{29}{12}$

$f(x)=x^2+\dfrac{29}{12},~g(x)=x-\dfrac{5}{6}$

が解となります。

参考

チャート式　数研出版

関連記事

スポンサーリンク