組分けの総数（組を区別しない場合）を求める際のポイント：場合の数

2016/3/2 2016/3/5 場合の数と確率, 数学, 数学A

1つ1つの組自体は区別せずに組分けをする問題です。
同じ人数(個数)を含む組がn組含まれるとき、組分けの方法は 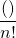$\dfrac{(区別するときの分け方)}{n!}$ となります。
複数個ずつ同じ人数になる組がある場合はそれぞれ別に考えます。

組分けの総数を求める問題

10人の生徒を3人、3人、2人、2人の4組に分ける方法は何通りあるか。

組を区別しない場合の解法の手順

それぞれの組を区別する場合の分け方を求めます。
3人の組が2つと2人の組が2つあるので、区別する場合の分け方を 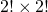$2!\times 2!$ で割ります。

組分けの総数を求める問題の解説

まずは組を区別する場合の分け方を求めます。
10人を3人ずつの2組と2人ずつの2組に分けるので、その分け方は

$~_{10}C_3 \times ~_7C_3 \times ~_4C_2 \times ~_2C_2$

$=\dfrac{10\times 9\times 8}{3\times 2\times 1}\times \dfrac{7\times 6\times 5}{3\times 2\times 1}\times \dfrac{4\times 3}{2\times 1}\times \dfrac{2\times 1}{2\times 1}$

$=120\times 35\times 6\times 1$

となります。
ここで、組を区別しない場合、3人ずつの2組について $2!$ 個の同じ組み合わせができることになり、
同様に2人ずつの2組についても $2!$ 個ずつの同じ組み合わせができることになります。
よって、全体では同じ組み合わせになるものは $2!\times 2!$ 存在することになるので、
組を区別しない場合の組分けの総数は

$\dfrac{120\times 35\times 6\times 1}{2!\times 2!}$

$=\dfrac{120\times 35\times 6\times 1}{4}$

$=6300$

存在することになります。

参考

数学A教科書　数研出版