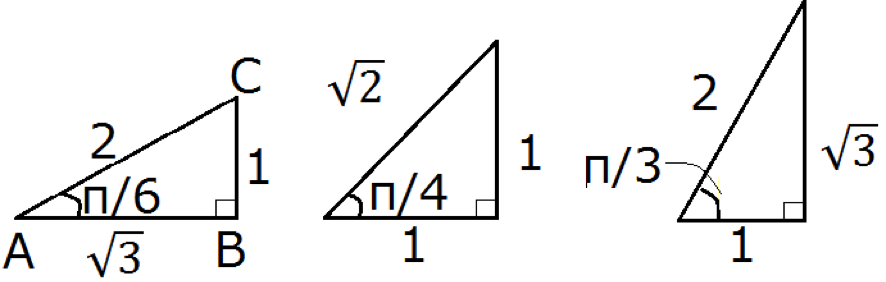三角比の一覧表（サイン、コサイン、タンジェントの値）：図形と計量

2015/10/9 2016/3/5 図形と計量, 数学, 数学Ⅰ

スポンサーリンク

三角比の一覧表（サイン、コサイン、タンジェントの値）

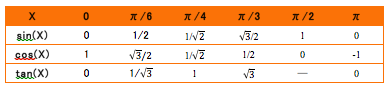
sin,cos,tanの主な角度での値はそれぞれ次の値をとります。

三角比の表

三角比の値（サイン、コサイン、タンジェントの値）の解説/ポイント

X=π/6, π/4, π/3 の時の三角形の辺の比

一つの角度が

$X=\dfrac{\pi}{6}, \dfrac{\pi}{4}, \dfrac{\pi}{3}$

となる直角三角形は上の図のような辺の長さの比になります。
たとえば, $X=\dfrac{\pi}{6}$ の時,

$sin(X)=\dfrac{BC}{AC}=\dfrac{1}{2}$

$cos(X)=\dfrac{AB}{AC}=\dfrac{~\sqrt[]{\mathstrut 3}}{2}$

$tan(X)=\dfrac{CB}{AB}=\dfrac{1}{~\sqrt[]{\mathstrut 3}}$

となります。

$X \geqq \dfrac{\pi}{2}$ の時は三角比の拡張で, 座標を用いた定義をします。

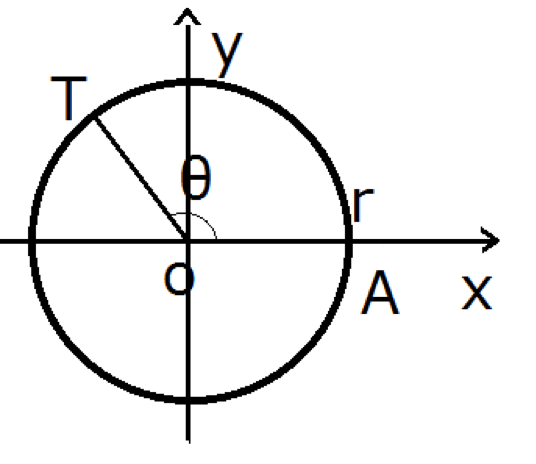
三角比の拡張

この図のように, 半径rの円周上に点Tをとり, その座標を(x, y)として, 各々を

$sin(\theta)=\dfrac{y}{r}$

$cos(\theta)=\dfrac{x}{r}$

$tan(\theta)=\dfrac{y}{x}$

と定義します。

たとえば, $\theta =\dfrac{\pi}{2}$ のときはTの座標は(0, r) と書けます。
よって,

$sin(\dfrac{\pi}{2})=1$

$cos(\dfrac{\pi}{2})=0$

となります。
ただし, tanについては分母が0となるため定義ができないことに注意しましょう。
同様にしてθ=πのときはTの座標は(-r, 0) と書けるので,

$sin(\pi)=0$

$cos(\pi)=-1$

$tan(\pi)=0$

となります。

参考

「数学Ⅰ　大島　利雄著　数研出版」

関連記事

スポンサーリンク