定積分の関数（上端・下端に文字を含む場合）の決定問題の解法ポイント

2016/3/2 2016/3/5 微分・積分, 数学, 数学Ⅱ

上端・下端に変数と定数が含まれる定積分で表された関数について、関数と定数の値を求める問題です。
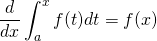$\dfrac{d}{dx} \displaystyle\int_a^xf(t)dt=f(x)$ から関数が求められます。
$\displaystyle\int_a^af(t)dt=0$ から定数の値が求められます。

スポンサーリンク

定積分の関数の決定問題

次の等式を満たす関数 $f(x)$ と、定数 $a$ を求めなさい。

$\int_a^xf(t)dt=x^2-5x+6$

上端・下端に文字を含む場合の解法の手順

両辺を微分して、 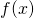$f(x)$ を求めます。
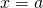$x=a$ を代入して、 $a$ の関係式を導きます。
関係式を解いて、 $a$ の値を求めます。

定積分の関数の決定問題の解説

$\int_a^xf(t)dt=x^2-5x+6$

に対して各辺を $x$ について微分すると

$f(x)=2x-5$

$(\because \dfrac{d}{dx} \int_a^xf(t)dt= f(x))$

となるので、
f(x)=2x-5と求められます。
次に、 $x=a$ を代入すると

$0=a^2-5a+6$

$(\because \int_a^af(t)dt=0 )$

が成り立つことになります。
これを解いて、

$(a-2)(a-3)=0$

より $a=2,3$ と求められます。

参考

数学2教科書　数研出版

関連記事

スポンサーリンク