- 平方根を含む数の、整数部分と小数部分を求める問題です。
![Rendered by QuickLaTeX.com ~\sqrt[]{\mathstrut n^2}< ~\sqrt[]{\mathstrut x}< ~\sqrt[]{\mathstrut (n+1)^2}](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-92401a2b66e89976f2d5e73914b11c89_l3.png) のとき、
のとき、![Rendered by QuickLaTeX.com ~\sqrt[]{\mathstrut x}](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-5e2a5ebd44eb3d89d194652d396c6673_l3.png) の整数部分は
の整数部分は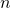 、小数部分は
、小数部分は![Rendered by QuickLaTeX.com ~\sqrt[]{\mathstrut x}-n](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-1c89c8210cce2f2b6c5810d592e09b2b_l3.png) となります。
となります。- 和・差はそのままずらしますが、整数倍は根号の中に入れて考えます。
スポンサーリンク
平方根(ルート)の整数部分と小数部分の値を求める問題
![]() の整数部分と小数部分を求めなさい。
の整数部分と小数部分を求めなさい。
整数部分と小数部分の値を求める解法の手順
![Rendered by QuickLaTeX.com 2 ~\sqrt[]{\mathstrut 7}](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-da9331065daf06e17504bf3aad563bf2_l3.png) の2を根号の中に入れます。
の2を根号の中に入れます。 - 根号で表された数を挟む2数を求めます。
- 2数のうち、小さい方が根号で表された数の整数部分となります。
- 3で求めた数に1を加えたものが元の数の整数部分となります。
- (元の数)-(整数部分)=(小数部分)となることを用いて小数部分を求めます。
平方根(ルート)の整数部分と小数部分の値を求める問題の解説
まず、![]() の整数部分を求めます。
の整数部分を求めます。
![]() より
より![]() なので
なので![]() の整数部分は2ですが、これを2倍すると
の整数部分は2ですが、これを2倍すると
![]() となってしまい、整数部分がうまく求められません。
となってしまい、整数部分がうまく求められません。
よって、![]() とすることで整数部分を求めます。
とすることで整数部分を求めます。
![]()
より
![]()
なので、![]() の整数部分は
の整数部分は![]() となります。
となります。
よって、![]() の整数部分は
の整数部分は![]()
次に、小数部分を求めます。
小数部分は、![]() であれば1の位の数である1を除いた
であれば1の位の数である1を除いた![]() の部分を表します。これは、元の数から整数部分を引くことで求められます。
の部分を表します。これは、元の数から整数部分を引くことで求められます。
![]() の整数部分は6なので、
の整数部分は6なので、
小数部分は
![]()
となります。
参考
チャート式 数研出版