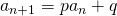 の形で表される、隣接2項間の漸化式から数列の一般項を求める問題です。
の形で表される、隣接2項間の漸化式から数列の一般項を求める問題です。 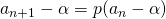 を満たす
を満たす 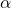 を求め、式を変形します。
を求め、式を変形します。 - 数列
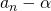 は等比数列になるので、等比数列の公式から一般項が求められます。
は等比数列になるので、等比数列の公式から一般項が求められます。
スポンサーリンク
隣接二項間漸化式の一般項を求める問題
![]()
![]() で定められる数列
で定められる数列![]() の一般項を求めなさい。
の一般項を求めなさい。
隣接二項間漸化式の一般項を求める解法の手順
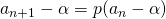 を満たす
を満たす 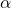 を求め、式を変形します。
を求め、式を変形します。 - 数列
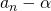 の初項となる、
の初項となる、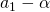 の値を求めます。
の値を求めます。 - 数列
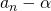 の一般項を、
の一般項を、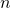 を用いた式で表します。
を用いた式で表します。 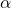 を移行することで、
を移行することで、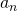 の一般項が表せます。
の一般項が表せます。
隣接二項間漸化式の一般項を求める問題の解説
![]() の係数が2なので、与えられた漸化式は
の係数が2なので、与えられた漸化式は
![]()
と変形できることになります。
展開して整理すると、
![]()
![]()
この式は元の漸化式![]() と等しいので、
と等しいので、![]() よって、
よって、
![]()
となります。
この漸化式から、数列![]() は公比が2の等比数列であり、初項は
は公比が2の等比数列であり、初項は
![]() なので、
なので、
![]()
左辺の![]() を移行して、
を移行して、
![]()
となります。
参考
数研出版 チャート式
2014年度京都大学入試問題