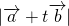 の形で表される、変数
の形で表される、変数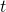 を含むベクトルの大きさの最大値や最小値を求める問題です。
を含むベクトルの大きさの最大値や最小値を求める問題です。 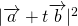 の値の変化を二次関数の最大・最小の考え方を利用して求め、その平方根をとります。
の値の変化を二次関数の最大・最小の考え方を利用して求め、その平方根をとります。
スポンサーリンク
ベクトルの大きさの最大値・最小値問題の問題
![]() ,
,![]() のとき、
のとき、![]() の最小値と、最小値をとるときのtの値を求めなさい。
の最小値と、最小値をとるときのtの値を求めなさい。
ベクトルの大きさの最大値・最小値問題の解法の手順
![Rendered by QuickLaTeX.com |\overrightarrow{a}+\overrightarrow{b} |=~\sqrt[]{\mathstrut 19}](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-83552662b7b8e9042b367732d7e55f5e_l3.png) の両辺を2乗して、内積
の両辺を2乗して、内積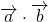 を求めます。
を求めます。 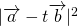 を展開します。
を展開します。 - 2で展開した式に1で求めた内積を代入して、
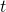 の二次関数を導きます。
の二次関数を導きます。 - 平方完成をして、
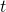 の二次関数の最小値を求めます。
の二次関数の最小値を求めます。 - 4で得られた最小値の平方根が、求めるベクトルの大きさの最小値となります。
ベクトルの大きさの最大値・最小値問題の解説
まずは与えられた条件式から、![]() を求めます。
を求めます。
![]() の両辺を2乗すると、
の両辺を2乗すると、
![]()
が得られます。これに![]() を代入して、
を代入して、
![]()
整理して
![]()
と求められます。
![]() に関しても、同様に2乗して内積を用いて表すと、
に関しても、同様に2乗して内積を用いて表すと、
![]()
![]()
となります。
これに![]() ,
,![]() と先に求めた
と先に求めた![]() を代入すると
を代入すると
![]()
![]()
となり、![]() の二次関数が得られます。
の二次関数が得られます。
この二次関数を平方完成すると
![]()
![]()
となるので、
![]() は
は![]() のとき最小値3をとります。
のとき最小値3をとります。
![]() の最小値が
の最小値が![]() なので、
なので、 ![]() より
より ![]() の最小値は
の最小値は
![]()
このとき![]() と求められます。
と求められます。
参考
チャート式 数研出版