常用対数を利用して、桁数を求める問題の解法ポイント：対数関数

2016/3/4 2016/3/5 指数関数と対数関数, 数学, 数学Ⅱ

スポンサーリンク

常用対数を利用して、桁数を求める問題の解法ポイント

常用対数を利用して、自然数の累乗の桁数を求める問題です。
桁数を求める数の常用対数をとり、その値を挟む2つの自然数を利用して桁数を求めます。

桁数を求める問題

$log_{10}2=0.3010$ とする。 $5^{10}$ は何桁の数になるか求めよ。

常用対数を利用しての解法の手順

常用対数 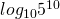$log_{10}5^{10}$ の値を求めます。
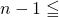$n-1 \leqq$ 桁数を求める数の常用対数 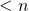$<n$ を満たす自然数 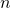$n$ を求めます。
求められた 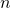$n$ が桁数となります。

桁数を求める問題の解説

$5^{10}$ を直接計算するのは難しいので、常用対数 $log_{10}5^{10}$ の値を求めます。

この問題では $5$ の常用対数の値が与えられていないので、
底である ${10}$ と常用対数の値が与えられている $2$ を使って
$5=\dfrac{10}{2}$ と表せることを利用します。

$log_{10}5^{10}$

$={10} log_{10}5$

$={10} log_{10}\dfrac{10}{2}$

$={10}(log_{10}{10}-log_{10}2 )$

$={10}(1-0.3010)$

$=6.99$

次に、得られた値を挟む $2$ つの自然数を求めると

$6 \leqq 6.99<7$

となります。よって、

$6 \leqq log_{10}5^{10} <7$

$log_{10}{10}^6 \leqq log_{10}5^{10} <log_{10}{10}^7$

${10}^6 \leqq 5^{10}<{10}^7$

となります。 ${10}^6$ は $7$ 桁の数であり、 ${10}^7$ は $8$ 桁で最小の数なので、
その間に存在する $5^{10}$ は7桁の数であることになります。

参考数学2教科書　数研出版

関連記事

スポンサーリンク