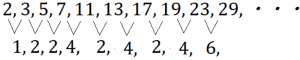数列とは（項・公差・公比・階差）：数列

2015/9/12 2016/3/5 数列, 数学, 数学B

数学Bの数列分野における、数列の概念や項、公差、公比、階差などの基本的な用語を確認します。

数列の具体例

数列

$\begin{eqnarray} &(1)& ~6,8,10,12,14,16,18,20,22,24,26, \dots \end{eqnarray}$

$\begin{eqnarray} &(2)& ~100,99,98,97,96,95,94,93,92,91, \dots \end{eqnarray}$

$\begin{eqnarray} &(3)& ~1,2,4,8,16,32,64,128,256,512,1024, \dots \end{eqnarray}$

$\begin{eqnarray} &(4)& ~2,3,5,7,11,13,17,19,23,29, \dots \end{eqnarray}$

$\begin{eqnarray} &(5)& ~1,2,2,4,2,4,2,4,6, \dots \end{eqnarray}$

について,
(1)~(3) の数列はそれぞれ(1) 初項6, 公差2の等差数列, (2) 初項100, 公差-1 の等差数列, (3) 初項1, 公比2 の等比数列と呼びます。
また, 数列(5) は数列(4) の階差数列になっています。

数列とはの解説・ポイント

まず, 数列とは $\begin{eqnarray} 2,3,5,7,11,13,17,19, \dots \end{eqnarray}$ このように数を一列に並べたものをいいます。
数列を構成している各数を数列の項と呼び最初の項から順番に第一項（初項）, 第二項, 第三項, ・・・といいます。
数列(1)(2) (3) のように隣り合う項同士の差（もしくは比）が一定の場合は, 等比数列（もしくは等比数列）といいます。
また, 数列(5) については,