- 2つのベクトルの内積を利用して、なす角を求める問題です。
- 2つのベクトル
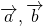 がなす角
がなす角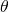 に関して、
に関して、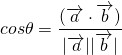 が成り立つことを利用します。
が成り立つことを利用します。
スポンサーリンク
なす角を求める問題
次の2つのベクトルのなす角![]() を求めなさい。
を求めなさい。
![]()
2つのベクトルの内積からなす角を求める解法の手順
- 2つのベクトルの大きさをそれぞれ求めます。
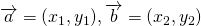 のとき、
のとき、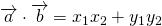 となることから内積を求めます。
となることから内積を求めます。 - なす角
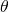 に関して
に関して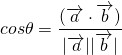 が成り立つことから
が成り立つことから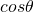 を求めます。
を求めます。 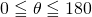 の範囲で、求められた
の範囲で、求められた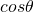 の値をとる角
の値をとる角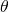 を求めます。
を求めます。
なす角を求める問題の解説
![]() の大きさは、それぞれ
の大きさは、それぞれ
![]()
![]()
となり、また、
![]()
![]()
![]()
![]()
となります。よって、![]() のなす角を
のなす角を![]() とすると、
とすると、
![Rendered by QuickLaTeX.com \[cos\theta=\dfrac{(\overrightarrow{a}\cdot \overrightarrow{b})}{|\overrightarrow{a} ||\overrightarrow{b} |}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-450a71772dbd7384361b9460b18d48d4_l3.png)
![]()
![]()
![]()
となります。
2つのベクトルのなす角は0°以上180°以下となるので、 この2つのベクトルのなす角は
![]()
![]()
と求められます。
参考
数学1 チャート式 数研出版