サイン(sin)、コサイン(cos)、タンジェント(tan)の意味と公式：図形と計量

三角比の定義

sin,cos,tanは次のように定義されます。

三角比の定義

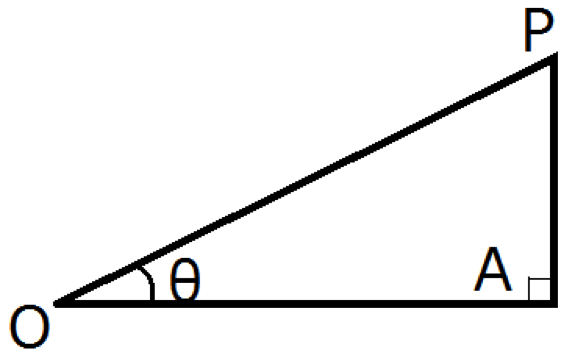
上図のように直角三角形OAPについて, $∠POA=\theta$ とします。ただし, $0<\theta < 90$ とします。
このとき, 各々の辺々の長さの比を

$sin\theta = \dfrac{AP}{OP}$

$cos\theta =\dfrac{OA}{OP}$

$tan\theta =\dfrac{AP}{OA}$

と定義します。

$sin\theta, ~cos\theta, ~tan\theta$ の値が, 用意する直角三角形によって変化するのではないかと不安になりますが, 実際は用意する直角三角形によらず同じ値をとります。

三角比の解説

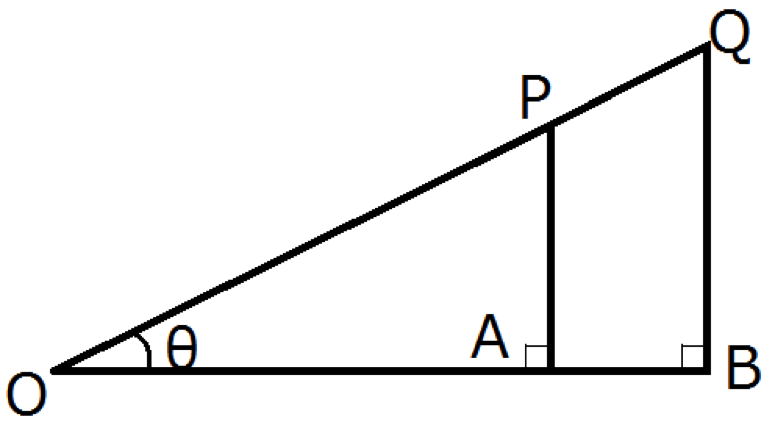
たとえば, 上図のように∠θが共通で異なる大きさの直角三角形OAPとOBQについて $cos\theta$ を考えます。

定義から△OAP,△ABQのそれぞれの場合の $cos\theta$ の値は

$cos\theta=\dfrac{OA}{OP}$

$cos\theta=\dfrac{OB}{OQ}$

になります。

ここで直角三角形OAPとOBQ は各々3つの角が同じ大きさをとっているので, △OAPと△OBQは相似です。

よってOA:OP=OB:OQつまり,

$\begin{eqnarray<em>} \dfrac{OA}{OP} =\dfrac{OB}{OQ} \end{eqnarray</em>}$

を満たします。

よって, 異なる直角三角形OAPとOBQであっても, $cos\theta$ 同じ値をとることがわかります。このことは, sinとtan にも同様のことがいうことができます。

「数学Ⅰ　大島　利雄著　数研出版」