円と２次関数の共有点の個数と座標を求めるポイント：図形と方程式

2016/3/1 2016/3/5 図形と方程式, 数学, 数学Ⅱ

円と放物線のような、曲線同士の共有点の個数と座標を求める問題です。
共有点の個数と座標は、1つの文字を消去した方程式の解から求められます。
1つの文字の値について、もう1つの文字に対応する値が存在するかに注意します。

スポンサーリンク

共有点の個数と座標を求める問題

円 $x^2+y^2=25$ と、放物線 $y=x^2-5$ の共有点の個数と座標を求めなさい。

円と２次関数の場合の解法の手順

放物線の式を 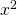$x^2$ について解きます。
1で解いた式を円の式に代入して、yの二次方程式を導きます。
二次方程式を解いて、yの値を求めます。
求められたyの値を放物線の式に代入して、xの値が存在するかを確かめます。
得られたxとyの値が共有点の座標、組の個数が共有点の個数となります。

共有点の個数と座標を求める問題の解説

図形の共有点を求める問題なので、直線同士の場合や直線と曲線の場合と同様に、
2つの式を連立方程式として解きます。円と放物線の場合、放物線の式をそのまま円の式に代入すると四次方程式になってしまうので、放物線の式を $x^2$ について解いて代入します。 $y=x^2-5$ を $x^2$ について解くと

$x^2=y+5$

となります。これを $x^2+y^2=25$ に代入すると

$y+5+y^2=25$

$y^2+y-20=0$

となり、yの二次方程式が得られます。この式を解くと、

$(y-4)(y+5)=0$

$y=4,-5$

となります。yの値が2つ得られたので、これらに対応するxの値が存在するかを確かめます。
$y=4$ を $y=x^2-5$ に代入すると、

$4=x^2-5$

$x^2=9$

$x=\pm 3$

となり、 $y=-5$ を代入すると

$-5=x^2-5$

$x^2=0$

$x=0$

となります。よって、連立方程式の解は

$(0,0),(3,4),(-3,4)$

の3組となります。
以上より、与えられた円と放物線の交点は3個で、座標はそれぞれ $(0,0),(3,4),(-3,4)$ となります。

参考

チャート式　数研出版

関連記事

スポンサーリンク