スポンサーリンク
二次関数の頂点の求め方の公式
![]() の頂点は
の頂点は
![]()
二次関数の頂点の求め方の解説/ポイント
二次関数の式を次のように平方完成します。
![]()
![]()
![]()
![]()
![]()
ここでたとえば, a>0 とすると,
このT は![]() のとき, つまり
のとき, つまり![]() で最小値をとります。
で最小値をとります。
このとき, Tの最小値は
![]()
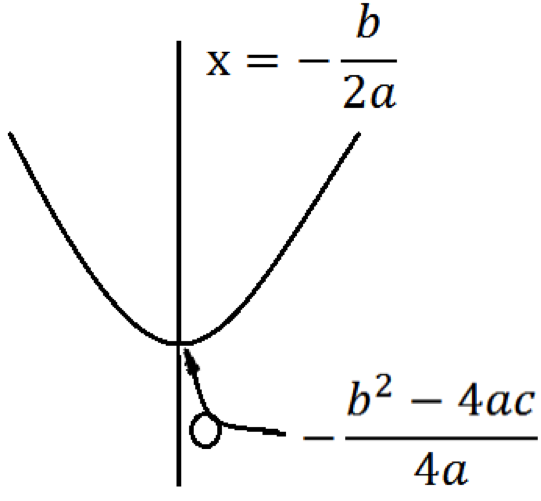
となります。 このことから, ![]() のグラフの頂点が
のグラフの頂点が
![]()
となることがわかります。
同様にしてa<0のときも, グラフの頂点が
![]()
となることがわかります。
覚えるときに符号を間違えないように注意してください。
二次関数の頂点の求め方の例題
問題
グラフ![]() の頂点を求めなさい。
の頂点を求めなさい。
解答
まず与えられた式を平方完成すると,
![]()
![]()
![]()
![]()
![]()
となるので頂点は(-2, 3) となります。
参考
「数学Ⅰ 大島 利雄著 数研出版」