スポンサーリンク
定義域内での最大値・最小値から二次関数を求めるポイント
- 定義域内での最大値と最小値が与えられた場合に、それを利用して二次関数を求める問題です。
- 定義域の端ではない部分で最大値または最小値をとる
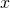 の値に着目します。
の値に着目します。
二次関数の決定問題
定義域が![]() のとき、
のとき、![]() で最小値
で最小値![]() をとり、最大値
をとり、最大値![]() をとる二次関数を求めなさい。
をとる二次関数を求めなさい。
定義域内での最大値・最小値から決定する解法の手順
- 定義域の端ではない部分での最大値、または最小値から頂点を求めます。
- 頂点の座標から二次関数の式を
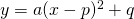 の形で表します。
の形で表します。 - もう一方の値をとる
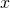 の値を求めます。
の値を求めます。 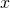 ともう一方の値から
ともう一方の値から の値を求めます。
の値を求めます。
二次関数の決定問題の解説
定義域の端ではない![]() のときに最小値
のときに最小値![]() をとるので、頂点は
をとるので、頂点は![]() となります。
となります。
よって、求める二次関数は![]() 、すなわち
、すなわち![]() と表せます。
と表せます。
また、頂点の位置で最小値をとるので![]() となります。
となります。
次に、最大値![]() をとる
をとる![]() の値を求めます。
の値を求めます。
![]() より、この二次関数は軸である
より、この二次関数は軸である![]() から離れるほど
から離れるほど![]() の値は大きくなります。
の値は大きくなります。
よって、最大値![]() をとるのは
をとるのは![]() のときとなります。
のときとなります。
![]() と
と![]() を
を![]() に代入して、
に代入して、
![]()
より
![]()
![]()
よって、求める二次関数は
![]() すなわち
すなわち![]() と求められます。
と求められます。
参考
数学1教科書 数研出版