恒等式の解法ポイント（複数の文字を含む場合）：式と証明

2016/3/2 2016/3/5 式と証明, 数学, 数学Ⅱ

複数の文字について恒等式が成り立つような、定数の値を求める問題です。
1種類の文字について恒等式が成り立つ場合と同様に、両辺の同類項を比較します。

スポンサーリンク

恒等式の問題

左辺

$(-x+3y+a)(2x+by+1)$

右辺

$-2x^2+cxy+6y^2+dx+ey-3$

の等式が $x$ と $y$ についての恒等式となるように、定数 $a,b,c,d,e$ の値を定めなさい。

複数の文字を含む場合の解法の手順

左辺を展開します。
両辺の同類項同士の係数が等しいことから、連立方程式をつくります。
連立方程式を解いて、 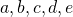$a,b,c,d,e$ の値を求めます。

恒等式の問題の解説

文字の種類が増えた場合でも、同類項同士の係数が等しくなることは変わらないので
両辺の係数を比較します。

左辺を展開すると、

$(-x+3y+a)(2x+by+1)$

$=-2x^2+(6-b)xy+3by^2+(2a-1)x+(ab+3)y+a$

となります。

与等式が恒等式になるとき、同類項同士の係数が等しくなるので
$6-b=c$ , $3b=6$ , $2a-1=d$ , $ab+3=e$ , $a=-3$
以上の5つの等式がすべて成り立ちます。

これらを解いて、

$a=-3,b=2,c=4,d=-7,e=-3$

が得られます。

参考

チャート式　数研出版

関連記事

スポンサーリンク