等差数列・等比数列・階差数列の公式まとめ：数列

2015/9/12 2016/3/5 数列, 数学, 数学B

スポンサーリンク

等差数列・等比数列・階差数列の公式まとめ

等差数列(1), 等比数列(2), 階差数列(3), を次のように定めます。

(1) 初項 $a$ ,公差 $d$ の等差数列
(2) 初項 $a$ ,公比 $r$ $(r\ne 1)$ の等比数列
(3) 初項 $b$ である数列 ${c_n}$ を階差数列とする数列

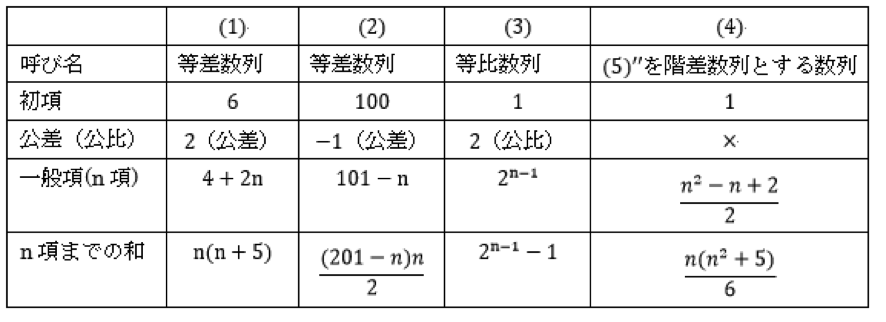
このとき, 一般項(n項)とn項までの和は次の表のようになります。

等差数列・等比数列・階差数列の一般項と和

等差数列・等比数列・階差数列の具体例

数列

$\begin{eqnarray<em>}&(1)& ~6,8,10,12,14,16,18,20,22,24,26,\dots\end{eqnarray</em>}$

$\begin{eqnarray<em>}&(2)& ~100,99,98,97,96,95,94,93,92,91,\dots\end{eqnarray</em>}$

$\begin{eqnarray<em>}&(3)& ~1,2,4,8,16,32,64,128,256,512,1024, \dots \end{eqnarray</em>}$

$\begin{eqnarray<em>}&(4)& ~ 1,2,4,7,11,16,22,29,37,46,56, \dots \end{eqnarray</em>}$

$\begin{eqnarray<em>}&(5)"& ~1,2,3,4,5,6,7,8,9,10, \dots \end{eqnarray</em>}$

を具体例に一般項と第n 項までの和を考えると,

一般項とn項までの和

このようになります。たとえば数列 (1) については, 初項a=6, 公差d=2 の等差数列になっていることに注意すると, 上の表より一般項は

$a+d(n-1)=6+2(n-1)=4+2n$

となります。
また, n項までの和は

$\dfrac{1}{2} n{2a+d(n-1)}$

$=\dfrac{1}{2} n{12+2(n-1)}$

$=n(n+5)$

となります。

数列(2),(3)についても初項と公差（もしくは公比)に数値を入れると出てきます。
数列(4) については, この場合階差数列が初項1,公差1 の等差数列になっている, つまり階差数列 ${c_n}$ の一般項は $c_n = n$ とかけます。
このことから求めたい数列(3) の一般項は

$\begin{eqnarray<em>}1+\sum_{k=1}^{n-1} n\end{eqnarray</em>}$

$\begin{eqnarray<em>}=1+\dfrac{n^2-n}{2}\end{eqnarray</em>}$

$\begin{eqnarray<em>}=\dfrac{n^2-n+2}{2}\end{eqnarray</em>}$

とかけます。

また, これより第n 項までの和は

$\begin{eqnarray<em>}\sum_{k=1}^{n} \dfrac{n^2-n+2}{2}\end{eqnarray</em>}$

$\begin{eqnarray<em>}= \dfrac{1}{2}\sum_{k=1}^{n} n^2 - \dfrac{1}{2}\sum_{k=1}^{n} n + \sum_{k=1}^{n} 1\end{eqnarray</em>}$

$\begin{eqnarray<em>}= \dfrac{1}{2} \dfrac{n(n+1)(2n+1)}{6} - \dfrac{1}{2} \dfrac{n(n+1)}{2} + n\end{eqnarray</em>}$

$\begin{eqnarray<em>}= \dfrac{n(n^2+5)}{6}\end{eqnarray</em>}$

とかけます。

参考

「数学B　坪井　俊著　数研出版」

関連記事

スポンサーリンク