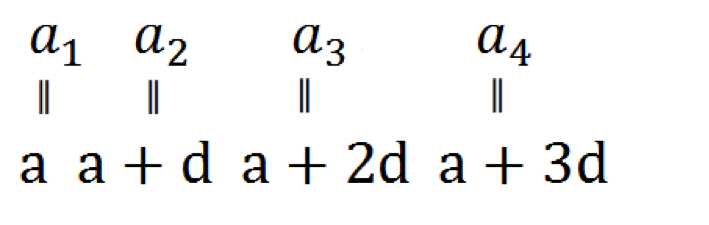等差数列の公式（一般項）の証明：数列

2015/9/12 2016/3/5 数列, 数学, 数学B

スポンサーリンク

等差数列の公式

初項a,公差d の等差数列 ${a_n}$ の一般項は

$\begin{eqnarray<em>} a_n=a+d(n-1) \end{eqnarray</em>}$

とかけます。

等差数列の公式（一般項）の証明の解説/ポイント

等差数列 ${a_n}$ は初項a,公差d の数列なので, $a_1, a_2, a_3, a_4$ を書き下すと

初項～第4項までの様子

このようになります。ここで, 公差が各々の隣り合う項の差つまり,

$\begin{eqnarray<em>} d=a_2-a_1=a_3-a_2=a_4-a_3= \dots \end{eqnarray</em>}$

をみたすことから,

$\begin{eqnarray<em>} a_1&=&a \end{eqnarray</em>}$

$\begin{eqnarray<em>}a_2 =&a_1+(a_2-a_1 ) \end{eqnarray</em>}$

$\begin{eqnarray<em>}=&a+d \end{eqnarray</em>}$

$\begin{eqnarray<em>}a_3 =&a_1+(a_2-a_1 )+(a_3-a_2 ) \end{eqnarray</em>}$

$\begin{eqnarray<em>}=&a+2d \end{eqnarray</em>}$

$\begin{eqnarray<em>}a_4 =&a_1+(a_2-a_1 )+(a_3-a_2 )+(a_4-a_3) \end{eqnarray</em>}$

$\begin{eqnarray<em>}=&a+3d \end{eqnarray</em>}$

となります。

同様にすると一般のn に対して,

$\begin{eqnarray<em>}a_n\end{eqnarray</em>}$

$\begin{eqnarray<em>}=&a_1+(a_2-a_1 )+(a_3-a_2 )+ \dots +(a_n-a_{n-1}) \end{eqnarray</em>}$

$\begin{eqnarray<em>}=&a+(n-1)d \end{eqnarray</em>}$

となります。

等差数列の公式の例題

問題

初項6, 公差2 の等差数列の一般項を求めなさい。

解答

初項a=6, 公差d=2 の等差数列になっていることに注意すると,一般項の公式より

$a_n$

$=a+d(n-1)$

$=6+2(n-1)$

$=4+2n$

となります。

参考

「数学B　坪井　俊著　数研出版」

関連記事

スポンサーリンク