スポンサーリンク
2点間の距離の公式
点A(a,c) と点B(b,d) の距離は
![\[\begin{eqnarray<em>} ~\sqrt[]{\mathstrut (b-a)^2+(d-c)^2} \end{eqnarray</em>}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-25b2da8113cdadd62b95f858914ddccc_l3.png "Rendered by QuickLaTeX.com")
となります。
2点間の距離の公式の求め方の解説/ポイント
2点間の距離の座標表示
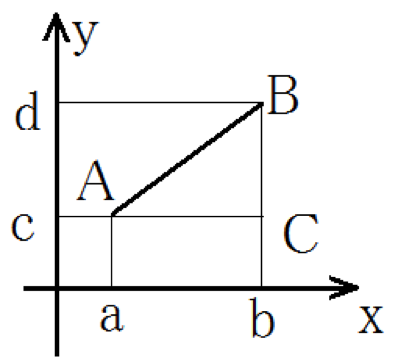
座標系で点Aと点Bを考えます。
また, 点Aと点Bの座標を用いて点C(b, c) とおきます。
ここで, 直角三角形ACBに三平方の定理を適応すると,
![\[\begin{eqnarray<em>} AB=~\sqrt[]{\mathstrut AC^2+BC^2}\end{eqnarray</em>}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-743937c0d83a4a0d27471db6b38b2b56_l3.png "Rendered by QuickLaTeX.com")
![\[\begin{eqnarray<em>} AB=~\sqrt[]{\mathstrut (b-a)^2+(d-c)^2} \end{eqnarray</em>}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-47197c0dd313fb876bb0130f083303ca_l3.png "Rendered by QuickLaTeX.com")
と書けます。
2点間の距離の公式の例題
問題
点A(2,3) と点B(4,5) の距離を求めなさい。
解答
2点間の距離の公式より
![\[\begin{eqnarray<em>} ~\sqrt[]{\mathstrut (4-2)^2+(5-3)^2} \end{eqnarray</em>}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-4cbb6f1f53b84057c2e47552eeff34c1_l3.png "Rendered by QuickLaTeX.com")
\begin{eqnarray}=~\sqrt[]{\mathstrut 8} \end{eqnarray}
![\[\begin{eqnarray<em>}=~2~\sqrt[]{\mathstrut 2} \end{eqnarray</em>}\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-827466335641efb90708a8385f8b54c8_l3.png "Rendered by QuickLaTeX.com")
となります。
参考
「新課程チャート式 基礎からの数学Ⅱ＋B チャート研究所編著 数研出版」