三角方程式（sin,cos）の解き方のポイント：三角関数

2016/3/4 2016/3/5 三角関数, 数学, 数学Ⅱ

スポンサーリンク

三角方程式（sin,cos）の解き方のポイント

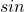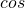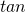$sin$ 、 $cos$ 、 $tan$ のうち2つ以上が含まれる三角方程式を解く問題です。
相互関係を用いて式に含まれる三角比を減らし、因数分解します。
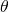$\theta$ の範囲によっては、解にならない値があることに注意します。

三角方程式の問題

次の三角方程式を解きなさい。ただし $0 \leqq \theta <180$ とします。

$2 cos^2\theta -sin\theta -1=0$

三角方程式の解法の手順

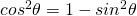$cos^2\theta =1-sin^2\theta$ を代入して、式を 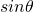$sin\theta$ だけで表します。
因数分解をして、 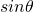$sin\theta$ の値を求めます。
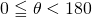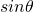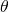$0 \leqq \theta <180$ の範囲で、求めた $sin\theta$ の値をとる $\theta$ を求めます。

三角方程式の問題の解説

複数の三角比が含まれる場合、相互関係を利用して種類を減らします。基本的に1次の $sin$ や $cos$ は変形が難しいので、次数が大きいものを1次の三角比に合わせて変形します。
この問題では1次の $sin\theta$ が含まれるので、 $2 cos^2\theta$ をそれに合わせて $sin\theta$ を含むように変形します。
相互関係より

$cos^2\theta =1-sin^2\theta$

なので、

$2 cos^2\theta -sin\theta -1=0は$

$2(1-sin^2\theta )-sin\theta -1=0$

$-2 sin^2\theta -sin\theta +1=0$

$2 sin^2\theta +sin\theta -1=0$

と変形できます。
方程式を $sin\theta$ だけで表せたので、通常の二次方程式と同じように因数分解をして $sin$ の値を求めると、

$(2 sin\theta -1)(sin\theta +1)=0より$

$sin\theta =\dfrac{1}{2},-1$

となります。
$0 \leqq \theta <180$ の範囲でこれらの値をとる $\theta$ を求めると、

$sin\theta =\dfrac{1}{2}$

のとき

$\theta =30,150$

となります。また、 $0 \leqq \theta <180$ の範囲では $sin\theta \geqq 0$ なので $sin\theta =-1$ を満たす $\theta$ は存在しません。
よって、解は

$\theta =30,150$

となります。

参考

チャート式　数研出版

関連記事

スポンサーリンク