ベクトルの垂直条件からなす角を求める問題のポイント

2つのベクトルの和や差に関する垂直条件から、2つのベクトルのなす角を求める問題です。
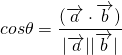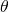垂直条件が成り立つときに内積が0になることを利用して、 $cos\theta =\dfrac{(\overrightarrow{a}\cdot \overrightarrow{b})}{|\overrightarrow{a} ||\overrightarrow{b}|}$ からなす角 $\theta$ を求めます。

ベクトルの垂直条件からなす角を求める問題

$\overrightarrow{a}+\overrightarrow{b}$ と $3\overrightarrow{a}-2\overrightarrow{b}、\overrightarrow{a}+2\overrightarrow{b}$ と $5\overrightarrow{a}-3\overrightarrow{b}$ がそれぞれ垂直であるとき、 $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角を求めなさい。

ベクトルのなす角を求める解法の手順

垂直であるとき内積が0になることから、与えられた条件を内積に関する式で表します。
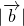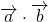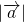2つの式を連立方程式として解き、 $|\overrightarrow{b} |$ と $\overrightarrow{a}\cdot \overrightarrow{b}$ を $|\overrightarrow{a} |$ を用いて表します。
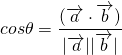$cos\theta =\dfrac{(\overrightarrow{a}\cdot \overrightarrow{b})}{|\overrightarrow{a} ||\overrightarrow{b}| }$ に2で得られた値を代入し、なす角 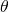$\theta$ を求めます。

ベクトルのなす角を求める問題の解説

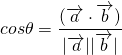なす角を求めるには、なす角 $\theta$ に関して $cos\theta =\dfrac{(\overrightarrow{a}\cdot \overrightarrow{b})}{|\overrightarrow{a} ||\overrightarrow{b}| }$ が成り立つことを利用します。
$\overrightarrow{a}+\overrightarrow{b}$ と $3\overrightarrow{a}-2\overrightarrow{b}、\overrightarrow{a}+2\overrightarrow{b}$ と $5\overrightarrow{a}-3\overrightarrow{b}$ がそれぞれ垂直であることから、

$(\overrightarrow{a}+\overrightarrow{b} )(3\overrightarrow{a}-2\overrightarrow{b} )=0$

$( \overrightarrow{a}+2\overrightarrow{b} )(5\overrightarrow{a}-3\overrightarrow{b} )=0$

が成り立ちます。これらの式を展開して整理すると、

$3|\overrightarrow{a}|^2+\overrightarrow{a}\cdot \overrightarrow{b}-2|\overrightarrow{b} |^2=0 \dots (1)$

$5|\overrightarrow{a} |^2+7\overrightarrow{a}\cdot \overrightarrow{b}-6|\overrightarrow{b} |^2=0 \dots (2)$

の2つの式が得られます。
未知数が3種類 $(|\overrightarrow{a}|,|\overrightarrow{b} |,\overrightarrow{a} \cdot \overrightarrow{b})$ 存在するのに対して式が2つなので
それぞれの値を求めることはできませんが、2種類を残りの1種類で表せれば、
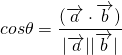$cos\theta =\dfrac{(\overrightarrow{a}\cdot \overrightarrow{b})}{|\overrightarrow{a} ||\overrightarrow{b}|}$ に代入してなす角が求められます。