スポンサーリンク
指数不等式の解法ポイント
- 変数
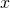 が累乗の指数の部分に含まれる、指数不等式を解く問題です。
が累乗の指数の部分に含まれる、指数不等式を解く問題です。 - 指数の底によっては、不等号の向きと指数の大小関係が変わることに注意します。
指数不等式の問題
指数不等式![]() を解きなさい。
を解きなさい。
指数不等式の解法の手順
- 指数の底を揃えます。
- 底の値に注意して、指数の大小関係に帰着させます。
指数不等式の解説
まずは指数の底を揃えます。![]() であることから、与不等式は
であることから、与不等式は
![]()
![]()
![]()
![]()
と変形できます。ここで、![]() なので、
なので、![]() の値は
の値は![]() が大きくなるほど小さくなります。
が大きくなるほど小さくなります。
よって、不等式![]() が成り立つのは
が成り立つのは
![]()
のときとなり、この不等式を解くと![]() より
より
![]()
が得られます。