最短経路（道順）を求める際のポイント（特定の通を通る場合）：場合の数

最短経路（道順）の問題

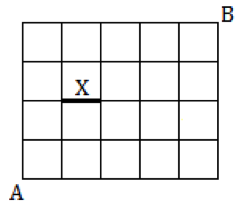
図のような格子状の道路がある。点Aから点Bまでの、通路Xを通らない最短経路を求めなさい。

最短経路の図

特定の通路を通らない場合は、余事象の考え方を用いて全体から通る場合を引くことで求めます。
まず、最短経路の総数を求めます。
点Aから点Bまでの最短経路は、上に4回と右に5回進むことになるので、その総数は

$\dfrac{9!}{5!4!}$

$=\dfrac{9\times 8\times 7\times 6}{4\times 3\times 2\times 1}$

$=126$

となります。

次に、点Xを通る最短経路の総数を求めます。
通路Xを通る最短経路なので、点A→通路Xの左側の点→通路X→通路Xの右側の点→点B
の順に進むことになります。
点Aから通路Xの左側の点までの最短経路は、上に2回と右に1回進むことになるので、
総数は

$\dfrac{3!}{2!1!}=3$

であり、通路Xの左側の点から通路Xを通って通路Xの右側の点に進む進み方は1通り、通路Xの右側の点から点Bまでの最短経路は、上に2回と右に3回進むことになるので、

$\dfrac{5!}{3!2!}=\dfrac{5\times 4}{2\times 1}=10$

となります。

よって、通路Xを通る最短経路は

$3\times 10=30$

存在することになります。

以上より、通路Xを通らない最短経路は

$126-30=96$

存在することが求められます。
通らない場合を求めるときは、特に最後の引き算を忘れないように注意が必要です。

チャート式　数研出版