恒等式の解法ポイント（複数の文字の条件式を含む場合）：式と計算

2016/3/2 2016/3/5 式と計算, 式と証明, 数学, 数学Ⅱ

条件式を満たす複数の文字の組について、式が恒等的に成り立つような定数の値を求める問題です。
条件式を利用して文字を消去することで、残った文字に関する恒等式に変形します。

スポンサーリンク

恒等式の問題

$3x+y-z=1$ , $x-y+3z=1$ を満たす $x,y,z$ に関して常に等式 $ax^2+by^2+cz^2=1$ が成り立つように、定数 $a,b,c$ の値を定めなさい。

複数の文字の条件式を含む場合の解法の手順

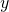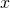条件式を連立方程式として解き、 $y$ , $z$ を $x$ を用いて表します。
1の結果を、 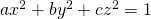$ax^2+by^2+cz^2=1$ に代入します。
2で得られた式は 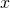$x$ についての恒等式となるので、同類項を比較して $a,b,c$ の値が定められます。

恒等式の問題の解説

条件式がある場合、条件式を利用して文字数を減らします。
$3x+y-z=1$ , $x-y+3z=1$ の両辺を足して、 $4x+2z=2$ より

$z=1-2x \dots (1)$

となります。

これを $3x+y-z=1$ に代入して、
$3x+y-(1-2x)=1$ より

$y=2-5x \dots (2)$

となります。

(1)、(2)を $ax^2+by^2+cz^2=1$ に代入することで、

$ax^2+b(2-5x)^2+c(1-2x)^2=1$

となり、式を $x$ だけで表すことができます。
ここでは $y,z$ を消去しましたが、どの文字を消去しても答えは得られるので
なるべく計算しやすいものを選びます。

ここで、(1)、(2)から1つの $x$ の値に関して対応する $y,z$ の値がそれぞれ1つずつ導けるので $x$ の値に関する条件は存在せず、すべての値をとることになります。

よって、 $ax^2+b(2-5x)^2+c(1-2x)^2=1$ は $x$ についての恒等式となります。

左辺を展開して整理すると、

$(a+25b+4c) x^2+(-20b-4c)x+4b+c=1$

が得られます。この式が $x$ についての恒等式となるので、両辺の同類項の係数を比較して

$a+25b+4c=0$

$-20b-4c=0$

$4b+c=1$

が成り立ちます。
これらの式を連立方程式として解いて、

$a=5,b=-1,c=5$

が得られます。

参考

チャート式　数研出版

関連記事

スポンサーリンク