内積成分表示の公式の証明：平面上ベクトル

ベクトルの内積の成分表示の公式

$\overrightarrow{a} = (a_1, a_2 ),\overrightarrow{b} = (b_1, b_2 )$ のとき, $\overrightarrow{a}$ と $\overrightarrow{b}$ の内積は

$\begin{eqnarray} \overrightarrow{a} \cdot \overrightarrow{b} = a_1b_1 +a_2b_2 \end{eqnarray}$

ベクトルの内積の成分表示の公式の証明/ポイント

重要なポイントは, ベクトルの内積は成分ごとの積の和になるということです。このとき, 添え字の順番を間違えないようにしましょう。

証明は, 内積の定義

$\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos\theta$

に立ち返ることがポイントになっています。

ベクトルの内積

$\overrightarrow{a},~ \overrightarrow{b} \ne \overrightarrow{0}$ かつ $\overrightarrow{a}$ と $\overrightarrow{b}$ は平行でないとします。

上の図のように $\overrightarrow{a}$ と $\overrightarrow{b}$ の始点を点Pとして, $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角を $\theta ~(0 \leqq \theta \leqq 180 ^{\circ})$ とします。　　　まず, 内積の定義より

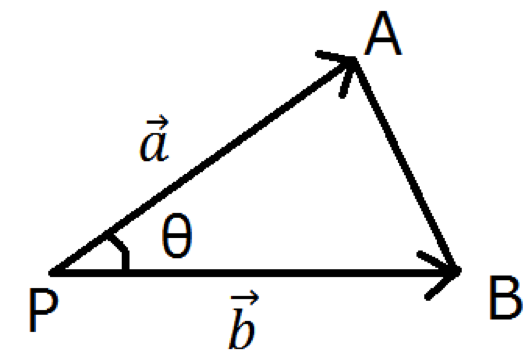
$\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos\theta$

と書けます。
また, 辺ABの長さは

$AB=|\overrightarrow{a}-\overrightarrow{b}|^2$

と書けることに注意すると,
△APBに対して, 余弦定理を適応すると,

$\begin{eqnarray} |\overrightarrow{a}|^2+|\overrightarrow{b}|^2-|\overrightarrow{a}-\overrightarrow{b}|^2=2|\overrightarrow{a}||\overrightarrow{b}|cos\theta \end{eqnarray}$

が成立します。
よって,

$\begin{eqnarray} \overrightarrow{a} \cdot \overrightarrow{b} =\dfrac{|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-|\overrightarrow{a}-\overrightarrow{b}|^2}{2} \end{eqnarray}$

と書くことができます。
ここで,

$|\overrightarrow{a}|^2, ~|\overrightarrow{b}|^2, ~|\overrightarrow{a}-\overrightarrow{b}|^2$

を各々ベクトル表記から座標に書き換えると,

$|\overrightarrow{a}|^2$

$=a_1^2+a_2^2, ~|\overrightarrow{b}|^2$

$=b_1^2+b_2^2, ~|\overrightarrow{a}-\overrightarrow{b}|^2$

$=(b_1-a_1)^2+(b_2-a_2)^2$

と書けます。よって,

$\begin{eqnarray} \overrightarrow{a} \cdot \overrightarrow{b}\end{eqnarray}$

$\begin{eqnarray}&=& \dfrac{(a_1^2+a_2^2)+( b_1^2+b_2^2)-{ (b_1-a_1)^2+(b_2-a_2)^2 }}{2}\end{eqnarray}$

$\begin{eqnarray}&=& \dfrac{2a_1b_1 +2a_2b_2 }{2}\end{eqnarray}$

$\begin{eqnarray}&=& a_1b_1 +a_2b_2 \end{eqnarray}$

$\overrightarrow{a}=\overrightarrow{0}$ もしくは $\overrightarrow{b}=\overrightarrow{0}$ のとき
$a_1,a_2=0$ もしくは $b_2,b_1=0$ となるので,
$\begin{eqnarray} a_1 b_1+a_2 b_2=0 \end{eqnarray}$ であり, かつ $\begin{eqnarray} \overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos\theta =0 \end{eqnarray}$ となるので,
この場合も