余弦定理の公式の証明：図形と計量

2015/10/9 2016/3/5 図形と計量, 数学, 数学Ⅰ

スポンサーリンク

余弦定理の公式

余弦定理

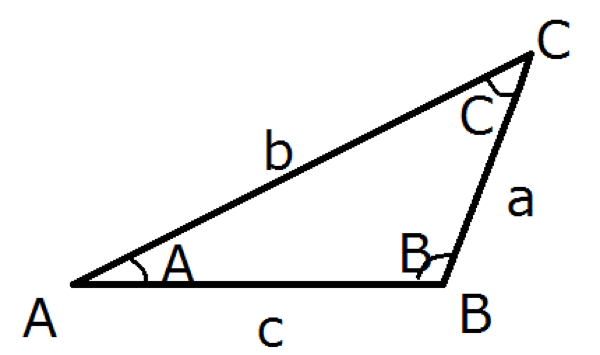
図のような三角形ABCに対して, 次の等式が成立します。これを余弦定理と呼びます。

$\begin{eqnarray<em>} a^2 = b^2 + c^2 -2bc cos A \end{eqnarray</em>}$

$\begin{eqnarray<em>} b^2 = c^2 + a^2 -2ca cos B \end{eqnarray</em>}$

$\begin{eqnarray<em>} c^2 = a^2 + b^2 -2ab cos C \end{eqnarray</em>}$

証明/ポイント

余弦定理の解説

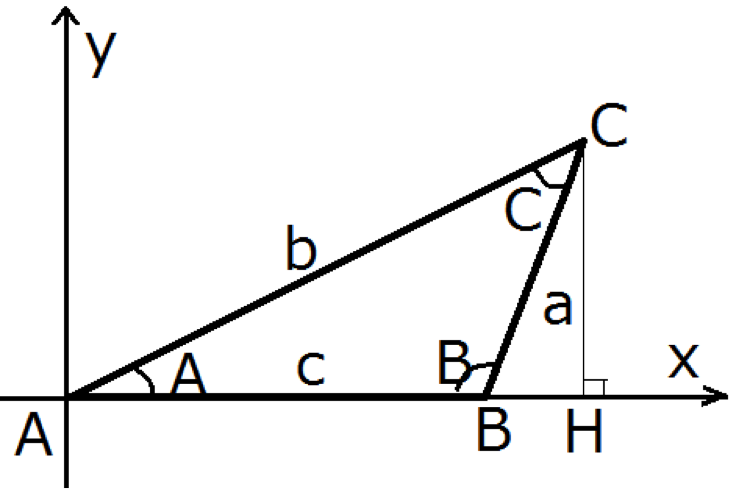
図のように点Aが原点となるようにxy座標をとり, 点Cからx軸に垂線をおろし, 足をHとします。
ここで, 長さCH, AHは各々

$CH=b sinA$

$AH=b cosA$

とかけます。

このことから, BH の長さは

$BH=|b cosA-c|$

と書けます。

ここで△BHCに対して三平方の定理を用いると,

$\begin{eqnarray<em>} a^2\end{eqnarray</em>}$

$\begin{eqnarray<em>}=(b ~sinA)^2+ | b ~cosA-c |^2 \end{eqnarray</em>}$

$\begin{eqnarray<em>}= (b ~sinA)^2 +(b ~cosA-c)^2 \end{eqnarray</em>}$

$\begin{eqnarray<em>}=b^2(sin^2 A+cos^2 A)+ c^2 - 2bc ~cosA\end{eqnarray</em>}$

$\begin{eqnarray<em>}= b^2+c^2-2bc ~cosA \end{eqnarray</em>}$

が導けます。
これは角Aが鈍角の場合も同じ証明で示すことができます。また, 座標のとり方を変えると同様にして, ほかの2つの式も導くことができます。

例題

問題

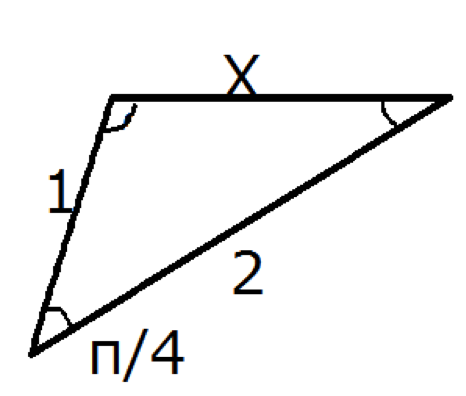
次の三角形のように辺の長さが1 と2 でその2つの辺で挟まれる角度が $\dfrac{\pi}{4}$ の時, Xの長さを求めなさい。

余弦定理の問題

解答

余弦定理より

$X^2$

$= 1^2+2^2-2 \times 1 \times 2\times cos(\dfrac{\pi}{4})$

$=5-2~\sqrt[]{\mathstrut 2}$

となるので, $X>0$ に注意して,

$X = ~\sqrt[]{\mathstrut 5-2~\sqrt[]{\mathstrut 2}}$

となります。

参考

「新課程チャート式基礎からの数学Ⅰ＋A チャート研究所編著数研出版」

関連記事

スポンサーリンク