三角関数の最大値・最小値を求める（定義域が与えられた場合）の解法ポイント

2016/3/2 2016/3/5 三角関数, 数学, 数学Ⅱ

スポンサーリンク

三角関数の最大値・最小値を求める（定義域が与えられた場合）の解法ポイント

与えられた定義域の中での、三角関数の最大値と最小値を求める問題です。
定義域から三角比の値の範囲を求めます。
二次関数の場合と同様に平方完成を行い、三角比の値の範囲から最大値と最小値を求めます。

三角関数の最大値・最小値を求める問題

$0\leqq \theta\leqq 90$ のときの、 $cos^2\theta-~\sqrt[]{\mathstrut 2} cos\theta+1$ の最大値、最小値とそのときの $\theta$ を求めなさい。

定義域が与えられた場合の解法の手順

定義域から 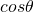$cos\theta$ の値の範囲を求めます。
与えられた式を平方完成します。
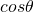$cos\theta$ の値の範囲から、最大値、最小値とそのときの 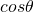$cos\theta$ の値を求めます。
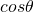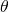三角方程式を解いて、 $cos\theta$ の値から $\theta$ を求めます。

三角関数の最大値・最小値を求める問題の解説

与えられた式は $cos$ の二次関数となっているので、まずは $cos\theta$ の値の範囲を求めます。
$0\leqq \theta\leqq 90$ なので、 $0\leqq cos\theta\leqq 1$ となります。
次に、この式を平方完成すると

$cos^2\theta-~\sqrt[]{\mathstrut 2} cos\theta+1$

$=\left(cos\theta-\dfrac{~\sqrt[]{\mathstrut 2}}{2}\right)^2-\dfrac{1}{2}+1$

$=\left(cos\theta-\dfrac{~\sqrt[]{\mathstrut 2}}{2}\right)^2+\dfrac{1}{2}$

となります。よって、 $0\leqq cos\theta\leqq 1$ において、
$cos\theta=\dfrac{~\sqrt[]{\mathstrut 2}}{2}$ のとき最小値

$\dfrac{1}{2}$

$cos\theta=0$ のとき最大値

$1$

をとります。

これらの値をとる $\theta$ を求めると、
$cos\theta=\dfrac{~\sqrt[]{\mathstrut 2}}{2}$ のとき $\theta=45$ であり、 $cos\theta=0$ のとき $\theta=90$ となります。
よって、
$cos\theta=\dfrac{~\sqrt[]{\mathstrut 2}}{2}$ すなわち $\theta=45$ のとき最小値 $\dfrac{1}{2}$ $cos\theta=0$ すなわち $\theta=90$ のとき最大値 $1$ と求められます。

最大値、最小値と $\theta$ を求める問題ですが、解答にはそのときの $cos\theta$ も付け加えると分かりやすく、確かめがしやすくなります。

参考

チャート式　数研出版

関連記事

スポンサーリンク