内積とベクトルの長さを求める際の解法ポイント：ベクトル

2016/3/4 2016/3/5 平面上のベクトル, 数学, 数学B

与えられた2つのベクトルの大きさと内積から、2つのベクトルの和や差の大きさを求める問題です。
内積を利用してベクトルの大きさの2乗を求め、その平方根をとります。

内積とベクトルの長さを求める問題

$| \overrightarrow{a} |=1,| \overrightarrow{b} |=3$ , $\overrightarrow{a} \cdot \overrightarrow{b} =2$ のとき、 $| \overrightarrow{a} -2 \overrightarrow{b} |$ を求めなさい。

内積とベクトルの長さを求める解法の手順

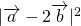$| \overrightarrow{a} -2 \overrightarrow{b} |^2$ を展開します。
展開した式に与えられたベクトルの大きさと内積を代入して、値を求めます。
求められた値の平方根をとります。

内積とベクトルの長さを求める問題の解説

ベクトルの大きさをそのまま求めるのは難しいので、まず大きさの2乗を求めます。

$| \overrightarrow{a} -2 \overrightarrow{b} |^2$

$=| \overrightarrow{a} |^2-4 \overrightarrow{a} \cdot \overrightarrow{b} +4| \overrightarrow{b} |^2$

なので、この式に $| \overrightarrow{a} |=1$ , $| \overrightarrow{b} |=3$ , $\overrightarrow{a} \cdot \overrightarrow{b} =2$ を代入して

$1^2-4\cdot 2+4\cdot 2^2=9$

となります。
$| \overrightarrow{a} -2 \overrightarrow{b} |^2=9$ であることと、 $| \overrightarrow{a} -2 \overrightarrow{b} |$ はベクトルの大きさなので $| \overrightarrow{a} -2 \overrightarrow{b} |>0$ であることから

$| \overrightarrow{a} -2 \overrightarrow{b} |=3$

と求められます。2乗から元の値を求めることを忘れないように注意します。

参考

数学B教科書　数研出版