スポンサーリンク
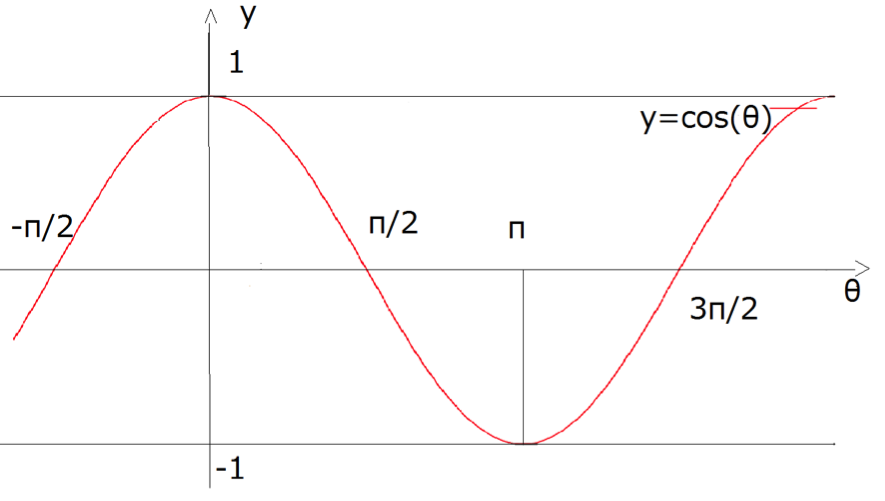
y=cos(θ) のグラフ (コサインのグラフ)
三角関数 y=cosx のグラフは次のように書けます。
y=cos(θ)のグラフ
y=cos(θ) のグラフの書き方 (コサインのグラフ)の解説/ポイント
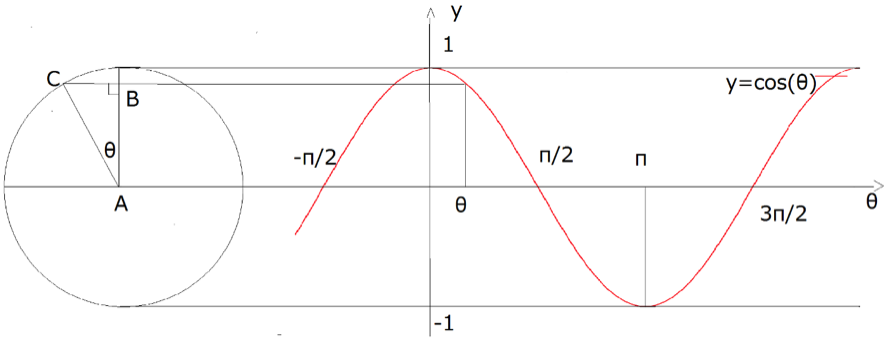
y=cos(θ) のグラフを書くときにはまず下の図のように単位円を描くと書きやすくなります。
y=cos(θ)のグラフの書き方
図のように単位円(半径1の円)に合わせて、三角形ABCをとり、ABとACの角度を![]() とおきます。
とおきます。
するとこの横に書いた円が単位円なので![]() に注意すると, 三角比の定義より
に注意すると, 三角比の定義より
![]()
![]()
![]()
![]()
と書けます。
ここで、ABを点Cのy 座標とみることもできます。よって、y=cos(θ) = (Cのy 座標) (ただし, θ は実数)とかけます。
上でBAの長さを点Cのy 座標と言い換えた理由は, そのままでは![]() の範囲以外では定義されていないためです。 というのもいままで三角比の定義で考えていた
の範囲以外では定義されていないためです。 というのもいままで三角比の定義で考えていた![]() は
は ![]() だけでした。
だけでした。
また, この三角関数のグラフから, ![]() や
や![]() となることが確認できます。
となることが確認できます。
y=cos(θ) のグラフの書き方 (コサインのグラフ)の例題
問題
![]() のグラフをもとに
のグラフをもとに![]() のグラフを書きなさい。
のグラフを書きなさい。
解答
三角関数の性質を思い出すと、
![]()
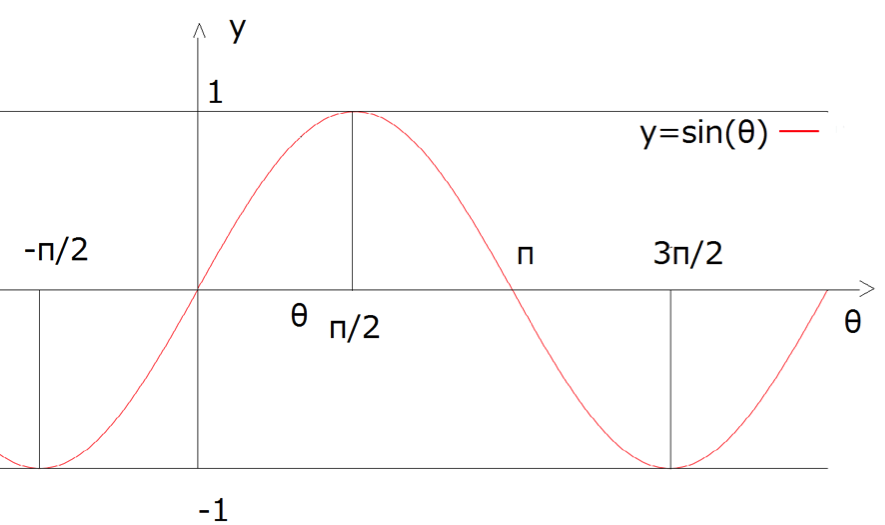
よって、上でみた![]() のグラフとは
のグラフとは ![]() 分ずれたグラフになるので下のようにかけます。
分ずれたグラフになるので下のようにかけます。
y=sin(θ)のグラフ
もしsinのグラフから ”+” 方向か ”-“ 方向のどちらかわからなくなってしまった場合は、sin(0)=0 になることを思い出すと間違えずに済むはずです。
参考
「数学Ⅱ 川中 宣明著 数研出版」