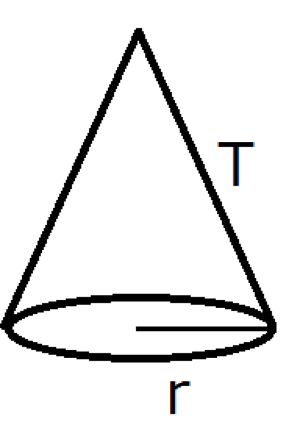
円錐の表面積の公式の求め方：中学数学

2015/10/9 2016/2/14 中学数学, 数学

円錐の表面積の公式

底面が半径rの円錐

図のような半径r の円を底面として母線がT の円錐の表面積S は

$\begin{eqnarray} S=\pi (r+T)r \end{eqnarray}$

と書けます。
ただし, πは円周率を指します。

底面が半径rの円錐の展開図

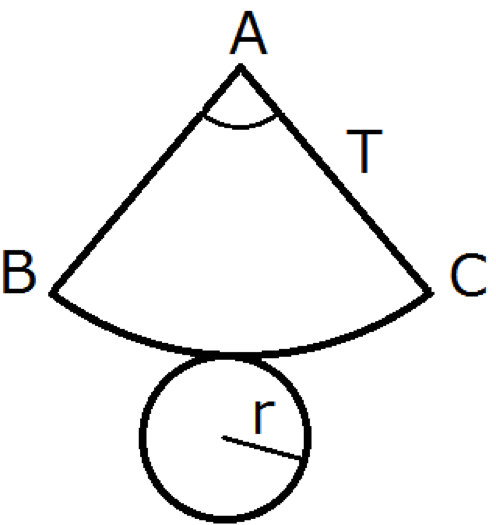
円錐の展開図は上図のようになります。まずポイントとなるのは扇の∠BACの大きさです。
半径r の円の円周と円弧BCの長さが一致するので

$\begin{eqnarray} 2r\pi = 2T\pi \dfrac{∠BAC}{360^{\circ} } \end{eqnarray}$

となります。つまり,

$∠BAC=\dfrac{r}{T}360^{\circ}$

であるので,扇部分ABCの面積をFとすると

$\begin{eqnarray}F=T^2\pi \dfrac{\dfrac{r}{T} 360^{\circ}}{360^{\circ}}\end{eqnarray}$

$\begin{eqnarray}F=Tr\pi \end{eqnarray}$

となります。また残る半径r の円の面積は $r^2 \pi$ なので,
求める表面積Sは

$\begin{eqnarray}S= Tr\pi + r^2\pi \end{eqnarray}$

$\begin{eqnarray}S= \pi (r + T) r\end{eqnarray}$

となります。

円錐の例

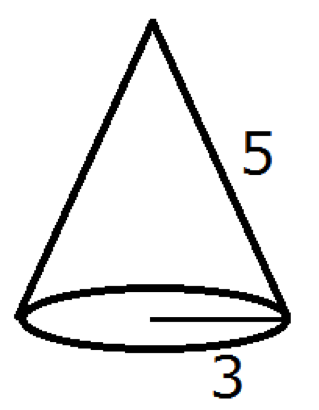
半径3 の円を底面として母線が5 の円錐の表面積Sを求めなさい。

円錐の表面積の公式より

$S= \pi (3+5)3 = 24 \pi$

となります。