3点を通る二次関数のグラフの決定のポイント：二次関数

2016/3/1 2016/3/13 2次関数と方程式・不等式, 二次関数, 数学, 数学Ⅰ

グラフが通る3点の座標から、二次関数を求める問題です。
一般形 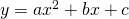$y=ax^2+bx+c$ に3点の座標を代入し、連立方程式として解きます。

スポンサーリンク

二次関数のグラフの決定の問題

グラフが $(2,3),(3,9),(4,19)$ の3点を通る二次関数の式を求めよ。

3点を通る場合の解法の手順

求める二次関数を 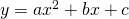$y=ax^2+bx+c$ とおきます。
3点の座標をそれぞれ代入します。
できた式を連立方程式として解きます。

二次関数のグラフの決定の問題の解説

まずは求める二次関数を文字を使って表します。
この問題のように頂点がわからない場合は $y=ax^2+bx+c$ とおきます。
次に、この式に3点の座標をそれぞれ代入します。
点 $(2,3)$ を通るので、 $x=2,y=3$ を代入して

$3=a∙2^2+b∙2+c$

整理して

$4a+2b+c=3 \dots (1)$

点 $(3,9),(4,19)$ を通ることから同様に

$9a+3b+c=9 \dots (2)$

$16a+4b+c=19 \dots (3)$

得られた関係式(1)、(2)、(3)を連立方程式として解いて、 $a,b,c$ の値を求めます。
この問題では係数がすべて同じ $c$ を消去し、 $a,b$ の値から求めるのが最も簡単です。

(2)－(1)より

$5a+b=6\dots (4)$

(3)－(2)より

$7a+b=10\dots (5)$

(5)－(4)より

$2a=4$

$a=2$

(4)に代入して、 $5\cdot 2+b=6$ より $b=-4$ となります。よって、 $a=2,b=-4$ を(1)に代入して、
$4\cdot 2+2\cdot (-4)+c=3$ より $c=3$ となります。

以上より、求める関数は

$y=2x^2-4x+3$

関連記事

スポンサーリンク