- 数列の第n項までの和を表す式から、数列の一般項を求める問題です。
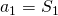 から初項を求め、
から初項を求め、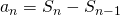 から第2項以降の項を求めます。
から第2項以降の項を求めます。 - 初項と第2項以降の項で求め方が異なるので、この2つが一致するか否かを判断します。
スポンサーリンク
Snから一般項を求める問題
第n項までの和が![]() で表される数列
で表される数列![]() の一般項を求めなさい。
の一般項を求めなさい。
初項から第n項までの和から一般項を求める手順
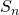 に
に 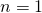 を代入して、
を代入して、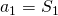 を求めます。
を求めます。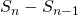 を計算して、
を計算して、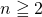 のときの
のときの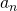 を求めます。
を求めます。 - 2で求めた
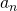 に
に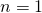 を代入して、1で求めた
を代入して、1で求めた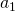 と比較します。
と比較します。
Snから一般項を求める問題の解説
まず、![]() は初項までの和なので初項
は初項までの和なので初項![]() と等しくなります。 よって、
と等しくなります。 よって、![]() に
に![]() を代入することで、
を代入することで、
![]()
が得られます。次に、![]() の場合、
の場合、![]() は第
は第![]() 項までの和から第
項までの和から第![]() 項までの和を引くことで求められます。
項までの和を引くことで求められます。
![]() のとき、
のとき、
![]()
![]()
![]()
![]()
![]()
![]()
となります。最後に、![]() のときの
のときの![]() に
に![]() を代入し、先に求めた
を代入し、先に求めた![]() と比較します。
と比較します。
![]() に
に![]() を代入すると
を代入すると
![]()
となるので、
![]() は
は![]() のときには成り立たないことになります。 このような場合は両方の式を記入し、
のときには成り立たないことになります。 このような場合は両方の式を記入し、
「![]() のとき
のとき![]() 」 のように答えます。
」 のように答えます。
参考
数学B教科書 数研出版