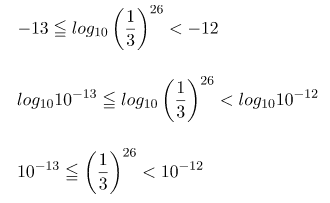常用対数を利用して、小数の第何位に0でない数字現れるかを求める問題のポイント：対数関数

2016/3/4 2016/3/5 指数関数と対数関数, 数学, 数学Ⅱ

小数や分数の累乗について、何桁目に初めて0でない数字が現れるかを求める問題です。
小数首位を求めよ、という表現がされる場合もあります。
位を求める数の常用対数をとり、その値を挟む2つの整数を利用して桁数を求めます。

スポンサーリンク

小数の第何位に0でない数字現れるかを求める問題

$\left( \dfrac{1}{3}\right)^{26}$ を小数で表すと、小数第何位に初めて $0$ でない数字が現れるか。
ただし、必要ならば $log_{10}3=0.4771$ として計算せよ。

《2014年度愛媛大学入試問題》

常用対数を利用する解法の手順

常用対数 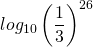$log_{10}\left( \dfrac{1}{3}\right)^{26}$ の値を求めます。
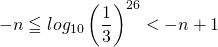$-n \leqq log_{10}\left( \dfrac{1}{3}\right)^{26} <-n+1$ となる自然数 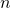$n$ を求めます。
求められた 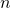$n$ が初めて0でない数字が現れる桁となります。

小数の第何位に0でない数字現れるかを求める問題の解説

$\left(\dfrac{1}{3}\right)^{26}$ を直接計算するのは難しいので、常用対数の値を求めます。
$\left(\dfrac{1}{3}\right)^{26}$ の常用対数の値を求めると、

$log_{10}\left( \dfrac{1}{3}\right)^{26}$

$={26} log_{10}\dfrac{1}{3}$

$=-{26} log_{10}3$

$=-{26}.4771$

$=-12.4046$

となります。
次に、求めた常用対数の値を挟む自然数を求めると、
$-13 \leqq -12.4046<-12$ となるので、

と変形できます。
${10}^{-13}$ は小数第 $13$ 位に初めて0でない数字が現れる最小の数であり、
${10}^{-12}$ は小数第12位に初めて0でない数字が現れる最小の数なので
この2つの数の間に存在する $\left( \dfrac{1}{3}\right)^{26}$ は小数第 $13$ 位に初めて0でない数字が現れる数となります。

参考

チャート式　数研出版

引用

2014年度愛媛大学入試問題

関連記事

スポンサーリンク