２次関数の決定（頂点の座標から）の解法ポイント：二次関数

2016/3/2 2016/3/5 2次関数と方程式・不等式, 二次関数, 数学, 数学Ⅰ

与えられた頂点の座標から二次関数を求める問題です。
求める二次関数を 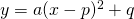$y=a(x-p)^2+q$ と置くことで頂点の座標を利用しやすくなります。

スポンサーリンク

２次関数の決定問題

頂点の座標が $(2,4)$ で、点 $(4,12)$ を通る二次関数を求めよ。

頂点の座標から決定する解法の手順

頂点の座標から、二次関数の式を 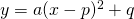$y=a(x-p)^2+q$ の形で表します。
もう1つの点の座標を代入します。
$a$ の値を求めます。

２次関数の決定問題の解説

頂点の座標をそのまま代入して関数を求めることができるので、二次関数の式を

$y=a(x-p)^2+q$

と置きます。
頂点の座標が $(2,4)$ なので、 $p=2,q=4$ を代入して

$y=a(x-2)^2+4$

となります。
点 $(4,12)$ を通るので、 $x=4,y=12$ を代入すると

$12=a(4-2)^2+4$

$12=4a+4$

$4a=8$

$a=2$

となるので、求める二次関数は

$y=2(x-2)^2+4$

となります。

参考

数学Ⅰ教科書　数研出版

関連記事

スポンサーリンク