- 文字定数を含む二次関数の最大値・最小値について、定数の値が変化するときの最大値・最小値を求める問題です。
- 平方完成で得られる最大値・最小値について、さらに平方完成をすることで求められます。
- 多変数の二次関数でも、同様の手順で最大値・最小値が求められます。
スポンサーリンク
二次関数の最大値・最小値の問題
![]() を定数とする。
を定数とする。![]() の二次関数
の二次関数![]() の最小値
の最小値![]() の最小値を求めなさい。
の最小値を求めなさい。
文字定数を含む場合の解法の手順
- 平方完成をして最小値
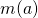 を求めます。
を求めます。 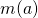 を
を の二次関数と考え、平方完成をして最小値を求めます。
の二次関数と考え、平方完成をして最小値を求めます。
二次関数の最大値・最小値の問題の解説
最大値・最小値に関する問題なので、まずは平方完成をします。
2種類の文字が含まれていますが、![]() の二次関数なので
の二次関数なので![]() について平方完成をします。
について平方完成をします。
![]()
![]()
![]()
となるので、二次関数![]() は
は
![]() のとき最小値
のとき最小値
![]()
をとります。
よって、![]() となります。
となります。
![]() は
は![]() の二次関数になっているので、その最小値も平方完成をすることで求められます。
の二次関数になっているので、その最小値も平方完成をすることで求められます。
![]()
![]()
![]()
となるので、![]() の最小値は
の最小値は![]() の時に
の時に![]() をとります。
をとります。
多変数関数の場合も、1つの文字を定数と考え、平方完成を繰り返すことで求められます。
参考
チャート式 数研出版