スポンサーリンク
点と直線の距離の公式
点A![]() と直線
と直線![]() の距離は
の距離は
![]()
となります。
点と直線の距離の公式の証明の解説/ポイント
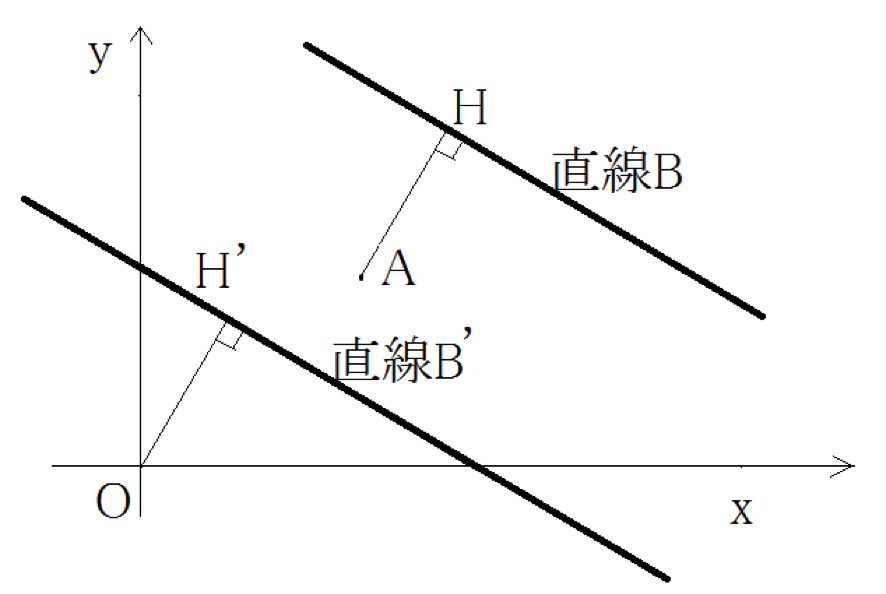
原点と直線の距離の公式から点Aを並行移動して、点と直線の距離の公式を導き出します。
直線BとOの距離 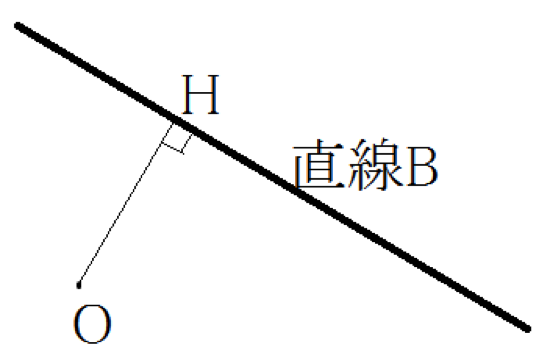
原点![]() と直線
と直線![]() の距離は
の距離は
![]()
となります。 原点と直線の距離の公式の証明は別記事で確認できます。
次に点A![]() と直線
と直線![]() の距離については
の距離については
図のようにまず点Aが原点に移るように全体を平行移動します。
この時直線Bを映したものを直線B’とすると![]() と書けます。
と書けます。
つまり
![]()
となります。 よって, 点A![]() と直線
と直線![]() の距離は
の距離は
原点![]() と直線
と直線![]() の距離とみることができるので,
の距離とみることができるので,
原点と直線の距離の公式より,
![]()
と書けます。
点と直線の距離の公式の例題
問題
原点![]() と直線
と直線 ![]() の距離を求めなさい。
の距離を求めなさい。
解答
点と直線の距離の公式より,
![]()
となります。
参考
「新課程チャート式 基礎からの数学Ⅱ+B チャート研究所編著 数研出版」