スポンサーリンク
3次関数の最大値・最小値を利用して、不等式を証明するポイント
- 3次関数に関する不等式を証明する問題です。
- 両辺の差を
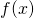 と置き、微分を利用して値の変化を調べます。
と置き、微分を利用して値の変化を調べます。
3次関数に関する不等式を証明する問題
![]() のとき、次の不等式が成り立つことを証明しなさい。
のとき、次の不等式が成り立つことを証明しなさい。
![]()
3次関数の不等式の証明の手順
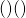 を
を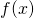 と置き、微分して増減を調べます。
と置き、微分して増減を調べます。 - 増減を元に、定義域内での
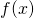 の最小値を求めます。
の最小値を求めます。 - 最小値を利用して
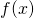 の不等式をつくります。
の不等式をつくります。 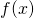 の不等式を移項して、与えられた不等式が成り立つことを示します。
の不等式を移項して、与えられた不等式が成り立つことを示します。
3次関数の不等式の証明の解説
3次以上の不等式を証明する場合、不等式の両辺の差を利用します。
両辺の差を求めると(左辺)-(右辺)は
![]()
![]()
となるので、![]() と置きます。
と置きます。
![]() の範囲で、
の範囲で、![]() の増減を調べると
の増減を調べると
![]()
![]()
![]()
より![]() が成り立つとき、
が成り立つとき、![]() であり、
であり、
![]()
![]()
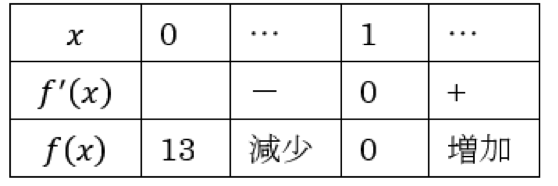
なので ![]() の増減は以下のようになります。
の増減は以下のようになります。
増減表より、![]() の範囲で
の範囲で![]() は
は![]() のとき最小値
のとき最小値![]() をとることが分かります。
をとることが分かります。
これを不等式で表すと、![]() の範囲で
の範囲で![]() 、すなわち
、すなわち
![]()
が成り立ちます。 元の不等式の右辺に含まれた項を移項することで
![]() となり、与不等式が成り立つことが示されます。
となり、与不等式が成り立つことが示されます。
参考
数学2教科書 数研出版