スポンサーリンク
二次関数のグラフの概形からa,b,c,の符号を決定するポイント
- 与えられた二次関数のグラフの概形から、文字定数の符号を求める問題です。
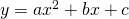 の
の 、
、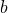 、
、 のほか、
のほか、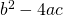 について問われる場合もあります。
について問われる場合もあります。 - グラフの向きと軸の位置、y切片の値に注目します。
グラフの概形か符号を決定する問題
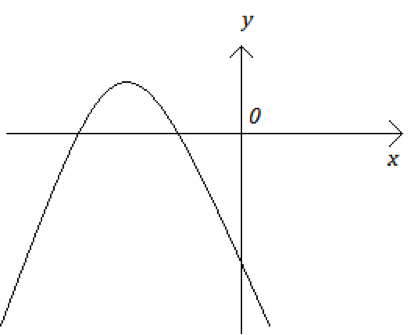
![]() のグラフが以下のようになるとき、
のグラフが以下のようになるとき、![]() 、
、![]() 、
、![]() 、
、![]() の符号が
の符号が
どのようになるかを答えなさい。
グラフの概形か符号を決定する解法の手順
- グラフの向きから
 の符号が求められます。
の符号が求められます。 - 軸の位置から
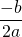 の符号が求められるので、これと
の符号が求められるので、これと の符号から
の符号から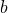 の符号を求めます。
の符号を求めます。 - y切片の位置から
 の符号が求められます。
の符号が求められます。 - グラフとx軸との交点の個数から
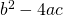 の符号が求められます。
の符号が求められます。
解説
まず、グラフの向きは上に凸なので、![]() であることがわかります。
であることがわかります。
次に、軸の位置は負の範囲にあるので、
![]()
![]()
より
![]() のグラフの軸は
のグラフの軸は![]() であることから
であることから
![]()
となります。 ![]() より
より![]() となります。 グラフの向きから
となります。 グラフの向きから![]() であることが求められているので
であることが求められているので![]() となります。
となります。
また、y切片(y軸との交点)が負の部分にあることから、![]() のとき
のとき![]() より
より![]() 、
、
グラフとx軸との交点が2つあるので(判別式)>0より
![]()
となります。以上より
![]()
参考
チャート式 数研出版