- 文字定数が含まれる三角方程式が、解を持つような文字定数の値の範囲を求める問題です。
- 解の存在を確かめる問題なので、判別式を利用します。
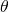 の値の範囲から三角比の値の範囲を求め、その値が解に含まれる条件を求めます。
の値の範囲から三角比の値の範囲を求め、その値が解に含まれる条件を求めます。
スポンサーリンク
文字の条件を決定する問題
方程式![]() が
が![]() の範囲で解を持つような
の範囲で解を持つような
定数![]() の値の範囲を求めなさい。
の値の範囲を求めなさい。
三角方程式が解を持つときの解法の手順
- xの値の範囲から
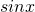 の値の範囲を求めます。
の値の範囲を求めます。 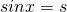 と置き換えます。
と置き換えます。 - 置き換えた方程式について、
 を含む項と含まない項に分けます。
を含む項と含まない項に分けます。  を含む項によって表される図形と、含まない項によって表される図形が交点を持つ条件を求めます。
を含む項によって表される図形と、含まない項によって表される図形が交点を持つ条件を求めます。
文字の条件を決定する問題の解説
まずは、![]() の値の範囲から
の値の範囲から![]() の値の範囲を求めます。
の値の範囲を求めます。
![]() なので、
なので、![]() となります。
となります。
![]() と置き換えると与方程式は
と置き換えると与方程式は
![]()
となります。この方程式について、![]() を含む項を右辺に移項すると
を含む項を右辺に移項すると
![]()
より
![]()
となり、方程式![]() が
が![]() の範囲に解を持つことは、
の範囲に解を持つことは、
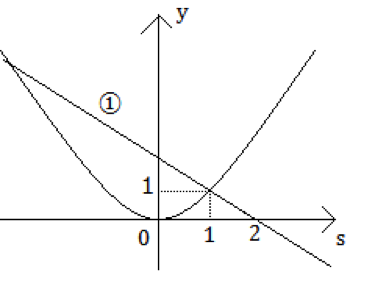
放物線![]() が直線
が直線![]() と
と![]() の範囲で交わることと同値となります。
の範囲で交わることと同値となります。
![]() の範囲でこの2つが交わる
の範囲でこの2つが交わる![]() の値の範囲は、
の値の範囲は、
関数の位置関係
直線![]() が点
が点![]() を通る①に重なるときと、s軸に一致するときの間となります。
を通る①に重なるときと、s軸に一致するときの間となります。
①に重なるとき、![]() を代入して
を代入して![]()
s軸に一致するとき、傾きが0になるので![]()
よって、
![]()
が求める範囲となります。
判別式とグラフの軸の位置を用いても求めることができますが、
このようにグラフを利用すると簡単に求められます。
参考
チャート式 数研出版