三角方程式の一般解を求める際のポイント：図形と計量

2016/3/1 2016/3/5 図形と計量, 数学, 鈍角の三角比

三角方程式の解を、一般解として表す問題です。
1つの解ごとに、周期の整数倍を加えることで一般解が表せます。

スポンサーリンク

三角方程式の一般解を求める問題

次の三角方程式の一般解を求めなさい。

$sin \left(2x+\dfrac{\pi}{6} \right)=\dfrac{~\sqrt[]{\mathstrut 3}}{2}$

三角方程式の一般解を求める解法の手順

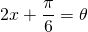$2x+\dfrac{\pi}{6}= \theta$ と置きます。
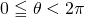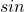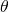$0 \leqq \theta<2\pi$ の範囲で、与えられた $sin$ の値をとる $\theta$ を求めます。
1で求めた 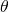$\theta$ に周期の整数倍を加えます。
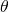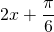$\theta$ を $2x+\dfrac{\pi}{6}$ に戻し、周期の整数倍を含む式を 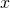$x$ について解きます。

三角方程式の一般解を求める問題の解説

まず $2x+\dfrac{\pi}{6}= \theta$ と置き、 $sin \theta =\dfrac{~\sqrt[]{\mathstrut 3}}{2}$ を満たす $\theta$ の値を求めます。

$sin \theta$ の周期が $2\pi$ であることから、 $0 \leqq \theta<2\pi$ の範囲で $sin \theta=\dfrac{~\sqrt[]{\mathstrut 3}}{2}$ を満たす $\theta$ の値を求めると

$\theta=\dfrac{\pi}{3},\dfrac{2}{3} \pi$

となります。ここで、 $sin \theta$ の周期は $2\pi$ なので、 $\theta=\dfrac{\pi}{3},\dfrac{2}{3} \pi$ に $2\pi$ の整数倍を加えたときにも、 $sin \theta=\dfrac{~\sqrt[]{\mathstrut 3}}{2}$ が成り立ちます。よって、整数 $n$ を用いて

$\theta=\dfrac{\pi}{3}+2n\pi, \dfrac{2}{3} \pi+2n\pi$

のときに $sin \theta=\dfrac{~\sqrt[]{\mathstrut 3}}{2}$ が成り立つ、と表せます。
$2x+\dfrac{\pi}{6}= \theta$ なので、 $\theta$ を $2x+\dfrac{\pi}{6}$ に戻すと

$2x+\dfrac{\pi}{6}$

$=\dfrac{\pi}{3}+2n\pi,~ \dfrac{2}{3} \pi+2n\pi$

となます。まず

$2x+\dfrac{\pi}{6}=\dfrac{\pi}{3}+2n\pi$

より

$2x=\dfrac{\pi}{6}+2n\pi$

$x=\dfrac{\pi}{6}+n\pi$

となります。また、

$2x+\dfrac{\pi}{6}=\dfrac{2}{3} \pi+2n\pi$

より

$2x=\dfrac{\pi}{2}+2n\pi$

$x=\dfrac{\pi}{4}+n\pi$

となります。よって、一般解は

$x=\dfrac{\pi}{6}+n\pi,\dfrac{\pi}{4}+n\pi$

と表せます。この問題のように $x$ の係数が1ではない場合、三角関数の周期と $x$ の周期が異なることに注意します。

参考

チャート式　数研出版

関連記事

スポンサーリンク