組分けの総数の求め方（区別がない場合）のポイント：場合の数

組分けの総数の求め方（区別がない場合）のポイント

• 果物やボールのように1つ1つを区別できない、同じものを分ける組分けの問題です。
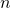• 組に分けることを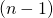個の仕切りを入れると考え、分けるものと仕切りの並べ方を考えます。

組分けの総数の問題

9個のリンゴを、3人で分ける。1個も貰わない人がいてもよい分け方と、
全員が少なくとも1個は貰う分け方はそれぞれ何通りあるか。

組分けの区別がない場合の解法手順

1. 9個を3人で分けるので、9個のと2本の仕切りの並べ方を考えます。
2. 全員が少なくとも1個は貰う場合、の間に仕切りを入れる方法を考えます。
3. 1個も貰わない人がいてもよい場合は、同じものを含む順列の考え方を利用します。

組分けの総数の問題の解説

3人で分ける場合、個の仕切りを入れると考え、9個のと2本の仕切りを並べます。
仕切りが端にある場合や連続で並ぶ場合が、1個も貰えない人がいる分け方を表します。
全員が少なくとも1個は貰う場合は、仕切りは端になく、連続して並ぶこともないので
9個のの間8ヵ所から2ヵ所を選んで仕切りを入れることになります。
よって、並べ方は

   

となります。
1個も貰わない人がいる分け方を含める場合、単に9個のと2個の仕切りを並べるので、
同じものを9個と2個、それぞれ含む順列の並べ方を考えて

   

となります。
よって、1個も貰わない人がいてもよい分け方は55通り、
全員が少なくとも1個は貰う分け方は28通りとなります。

参考

チャート式　数研出版