隣接3項間漸化式の一般項を求める際のポイント（特性方程式が重解を持つ場合）：数列

2016/3/2 2016/3/4 数列, 数学

スポンサーリンク

隣接3項間漸化式の一般項を求める際のポイント（特性方程式が重解を持つ場合）

隣接3項間の漸化式から一般項を求める問題について、特性方程式が重解を持つ場合です。
特性方程式から得られる隣接2項間の漸化式を変形して一般項を求めます。

隣接3項間漸化式の一般項を求める問題

$a_1=1$ , $a_2=4$ , $a_{n+2}=6a_{n+1}-9a_n$ を満たす数列 ${a_n}$ の一般項を求めなさい。

特性方程式が重解を持つ場合の解法の手順

特性方程式を解きます。
特性方程式の重解 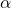$\alpha$ を利用して、漸化式を変形します。
変形した漸化式から、隣接2項間の漸化式を導きます。
隣接2項間の漸化式の両辺を 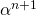$\alpha ^{n+1}$ で割ります。
4で得られた漸化式から、数列 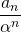${\dfrac{a_n}{\alpha ^n} }$ の一般項を求めます。
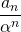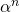$\dfrac{a_n}{\alpha ^n}$ の一般項を $\alpha ^n$ 倍することで、元の数列 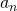${a_n }$ の一般項が求められます。

隣接3項間漸化式の一般項を求めるの解説

$a_{n+2}=6a_{n+1}-9a_n$ の特性方程式である $x^2=6x-9$ を解くと、

$x^2-6x+9=0$

$(x-3)^2=0$

より $x=3$ が重解となります。よって、与えられた漸化式は

$a_{n+2}-3a_{n+1}$

$=3(a_{n+1}-3a_n )$

と変形されます。

$b_n=a_{n+1}-3a_n$ と置くと、

$b_1=a_2-3a_1$

$=4-3$

$=1$

であり、

$a_{n+2}-3a_{n+1}$

$=3(a_{n+1}-3a_n )$

より

$b_{n+1}=3b_n$

となるので、数列 ${b_n }$ は初項1、公比3の等比数列となります。
よって、

$b_n=3^{n-1}$

と表せます。
この式に $b_n=a_{n+1}-3a_n$ を代入すると

$a_{n+1}-3a_n=3^{n-1}$

が得られます。
特性方程式が重解を持つ場合は隣接2項間の漸化式が1通りしか得られないので、
この漸化式を変形して一般項を導きます。
漸化式の両辺を $3^{n+1}$ で割ると、

$\dfrac{a_{n+1}}{3^{n+1}} -\dfrac{ 3a_n}{3^{n+1}}$

$=\dfrac{3^{n-1}}{3^{n+1}}$

より

$\dfrac{a_{n+1}}{3^{n+1}} -\dfrac{a_n}{3^n}$

$=\dfrac{1}{9}$

となります。

ここで、 $c_n=\dfrac{a_n}{3^n}$ と置くと、

$c_{n+1}-c_n=\dfrac{1}{9}$

となり、 $c_1=\dfrac{a_1}{3}=\dfrac{1}{3}$ であることから数列 ${c_n }$ は初項 $\dfrac{1}{3}$ 、公差 $\dfrac{1}{9}$ の等差数列となります。
よって、

$c_n=\dfrac{1}{3}+\dfrac{1}{9} (n-1)$

$= \dfrac{1}{9} n+\dfrac{2}{9}$

$c_n=\dfrac{a_n}{3^n}$ より

$\dfrac{a_n}{3^n} = \dfrac{1}{9} n+\dfrac{2}{9}$

となるので、

$a_n=3^n \left(\dfrac{1}{9} n+\dfrac{2}{9} \right)$

$=n∙3^{n-2}+2\cdot 3^{n-2}$

と求められます。

参考

チャート式　数研出版

関連記事

スポンサーリンク