2次の対数方程式（log）の解き方のポイント：対数関数

2016/3/4 2016/3/13 指数関数と対数関数, 数学, 数学Ⅱ

スポンサーリンク

2次の対数方程式（log）の解き方のポイント

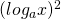$(log_ax )^2$ が含まれる、2次の対数方程式を解く問題です。
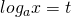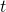$log_ax=t$ として、 $t$ の2次方程式に置き換えて解きます。

2次の対数方程式の問題

方程式 $(log_3x )^2+log_3x^2 -8=0$ を解け。

2次の対数方程式の解法の手順

最初に、真数条件から解の値の範囲を求めます。
方程式中の対数をすべて 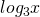$log_3x$ を用いて表します。
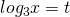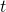$log_3x=t$ として、 $t$ の2次方程式に置き換えます。
2次方程式を解いて 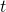$t$ の値を求めます。
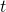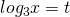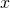求められた $t$ の値について、対数方程式 $log_3x=t$ を満たす $x$ を求めます。

2次の対数方程式の問題の解説

まずは真数条件を用いて解の値の範囲を求めます。
$x>0,x^2>0$ より $x>0$ がこの方程式の解の値の範囲となります。
次に、対数の2乗を含む項 $(log_3x )^2$ があるので、他の項を $log_3x$ で表される形に変形します。

$(log_3x )^2+log_3x^2 -8=0より$

$(log_3x )^2+2 log_3x-8=0$

と変形できます。ここで、 $log_3x=t$ とおくと、
対数方程式が $t$ の2次方程式

$t^2+2t-8=0$

に置き換えられます。この2次方程式を解くと、

$(t+4)(t-2)=0$

より $t=-4,2$ よって、 $t$ を元に戻すと

$log_3x=-4,2$

より

$x=3^{(-4)}= \dfrac{1}{3^4} =\dfrac{1}{81}$

$x=3^2=9$

となります。
この2つの解は解の値の範囲である $x>0$ に含まれるので、解は

$x=\dfrac{1}{81},9$

となります。

参考

チャート式　数研出版

関連記事

スポンサーリンク